Algebra
-
If 1 = 1 + 1 + 1 ;
a + b ≠ 0, then x = ?a + b + x a b x
-
View Hint View Answer Discuss in Forum
1 − 1 = 1 + 1 a + b + x x a b ⇒ x − (a + b + x) = a + b x(a + b + x) ab ⇒ − (a + b) = a + b x(a + b + x) ab
⇒ – ab (a + b) = (a + b) x (a + b + x)
⇒ (a + b) {x (a + b + x) + ab} = 0
⇒ x (a + b + x) + ab = 0
[∵ a + b ≠ 0]
⇒ x2 + ax + bx + ab = 0
⇒ x (x + a) + b (x + a) = 0
⇒ (x + a) (x + b) = 0
⇒ x = –a or, –bCorrect Option: C
1 − 1 = 1 + 1 a + b + x x a b ⇒ x − (a + b + x) = a + b x(a + b + x) ab ⇒ − (a + b) = a + b x(a + b + x) ab
⇒ – ab (a + b) = (a + b) x (a + b + x)
⇒ (a + b) {x (a + b + x) + ab} = 0
⇒ x (a + b + x) + ab = 0
[∵ a + b ≠ 0]
⇒ x2 + ax + bx + ab = 0
⇒ x (x + a) + b (x + a) = 0
⇒ (x + a) (x + b) = 0
⇒ x = –a or, –b
-
If 5 + 2√3 = a + b√3, the values of a and b respectively are : 7 + 4√3
-
View Hint View Answer Discuss in Forum
Expression = 5 + 2√3 7 + 4√3 = 5 + 2√3 × 7 − 4√3 7 + 4√3 7 − 4√3
Rationlising the denominator= 5 × 7 − 5 × 4√3 + 2√3 × 7 − 2√3 × 4√3 72 − (4√3)2 = 35 − 20√3 + 14√3 − 24 49 − 48
= 11 – 6√3∴ 5 + 2√3 = a + b√3 7 + 4√3
⇒ a + b√3 = 11 – 6√3
⇒ a = 11, b = –6Correct Option: B
Expression = 5 + 2√3 7 + 4√3 = 5 + 2√3 × 7 − 4√3 7 + 4√3 7 − 4√3
Rationlising the denominator= 5 × 7 − 5 × 4√3 + 2√3 × 7 − 2√3 × 4√3 72 − (4√3)2 = 35 − 20√3 + 14√3 − 24 49 − 48
= 11 – 6√3∴ 5 + 2√3 = a + b√3 7 + 4√3
⇒ a + b√3 = 11 – 6√3
⇒ a = 11, b = –6
-
If x = 1 , what will be the value of x3 − – 2x2 – 7x + 5 ? 2 − √3
-
View Hint View Answer Discuss in Forum
x = 1 2 − √3 = 1 × 2 + √3 2 − √3 2 + √3 = 2 + √3 × 2 + √3 22 − (√3)2 4 − 3
= 2 + √3
⇒ x – 2 = √3
On squaring both sides,
⇒ (x – 2)2 = (√3)2
⇒ x2 – 4x + 4 = 3
⇒ x2 – 4x + 1 = 0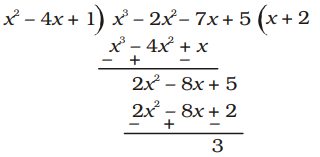
∴ x3 – 2x2 – 7x + 5 = (x2 – 4x +1) (x + 2) + 3 = 0 + 3 = 3Correct Option: C
x = 1 2 − √3 = 1 × 2 + √3 2 − √3 2 + √3 = 2 + √3 × 2 + √3 22 − (√3)2 4 − 3
= 2 + √3
⇒ x – 2 = √3
On squaring both sides,
⇒ (x – 2)2 = (√3)2
⇒ x2 – 4x + 4 = 3
⇒ x2 – 4x + 1 = 0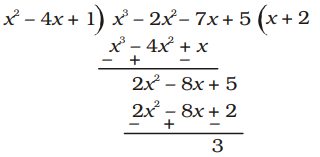
∴ x3 – 2x2 – 7x + 5 = (x2 – 4x +1) (x + 2) + 3 = 0 + 3 = 3
-
If x4 + 1 = 47, what will be the value of x3 + 1 ? x4 x3
-
View Hint View Answer Discuss in Forum
x4 + 1 = 47 x4 ⇒ (x2)2 
1 
2 = 47 x2 ⇒ 
x2 + 1 
2 – 2 = 47 x2
[∵ a2 + b2 = (a + b)2 – 2ab]⇒ 
x2 + 1 
2 = 47 + 2 = 49 x2 ⇒ x2 + 1 = √49 = 7 x2 Again, 
x + 1 
2 – 2 = 7 x ⇒ 
x + 1 
2 = 7 + 2 = 9 x ⇒ x + 1 = √9 = 3 x
On cubing both sides,
x + 1 
3 = 33 x ⇒ x3 + 1 + 3 
x + 1 
= 27 x3 x ⇒ x3 + 1 + 3 × 3 = 27 x3 ⇒ x3 + 1 = 27 – 9 = 18 x3 Correct Option: A
x4 + 1 = 47 x4 ⇒ (x2)2 
1 
2 = 47 x2 ⇒ 
x2 + 1 
2 – 2 = 47 x2
[∵ a2 + b2 = (a + b)2 – 2ab]⇒ 
x2 + 1 
2 = 47 + 2 = 49 x2 ⇒ x2 + 1 = √49 = 7 x2 Again, 
x + 1 
2 – 2 = 7 x ⇒ 
x + 1 
2 = 7 + 2 = 9 x ⇒ x + 1 = √9 = 3 x
On cubing both sides,
x + 1 
3 = 33 x ⇒ x3 + 1 + 3 
x + 1 
= 27 x3 x ⇒ x3 + 1 + 3 × 3 = 27 x3 ⇒ x3 + 1 = 27 – 9 = 18 x3
-
If x x − bc + x − ca + x − ab = a + b + c what is the value of x ? b + c c + a a + b
-
View Hint View Answer Discuss in Forum
x − bc + x − ca + x − ab = a + b + c b + c c + a a + b ⇒ x − bc − a + x − ca − b + x − ab − c = 0 b + c c + a a + b ⇒ x − bc − ab − ac + x − ca − bc − ab + x − ab − ac − bc = 0 b + c c + a a + b
⇒ x – bc – ab – ac = 0
⇒ x = ab + bc + acCorrect Option: D
x − bc + x − ca + x − ab = a + b + c b + c c + a a + b ⇒ x − bc − a + x − ca − b + x − ab − c = 0 b + c c + a a + b ⇒ x − bc − ab − ac + x − ca − bc − ab + x − ab − ac − bc = 0 b + c c + a a + b
⇒ x – bc – ab – ac = 0
⇒ x = ab + bc + ac

