Mensuration
- The radius of a circle is so increased that its circumference increases by 5%. The area of the circle then increases by:
-
View Hint View Answer Discuss in Forum
Increase in radius of circle = Increase in circumference of circle = 5%
∴ Increase in area = 
5 + 5 + 5 × 5 
% = 10.25% 100 Correct Option: B
Increase in radius of circle = Increase in circumference of circle = 5%
∴ Increase in area = 
5 + 5 + 5 × 5 
% = 10.25% 100
- The base of a right prism is a rightangled triangle whose sides are 5 cm, 12 cm and 13 cm. If the area of the total surface of the prism is 360 cm², then its height (in cm) is
-
View Hint View Answer Discuss in Forum
Total surface area = Lateral surface area + 2 Area of base = Area of base × height + area of base
⇒ 360 = 30 × h + 1 × 5 × 12 2
⇒ 360 – 30 = 30 × h
⇒ 30h = 330⇒ h = 300 = 10 cm. 30 Correct Option: A
Total surface area = Lateral surface area + 2 Area of base = Area of base × height + area of base
⇒ 360 = 30 × h + 1 × 5 × 12 2
⇒ 360 – 30 = 30 × h
⇒ 30h = 330⇒ h = 300 = 10 cm. 30
- The area of a rhombus is 216 cm² and the length of its one diagonal is 24 cm. The perimeter (in cm) of the rhombus is
-
View Hint View Answer Discuss in Forum
Using Rule 12,
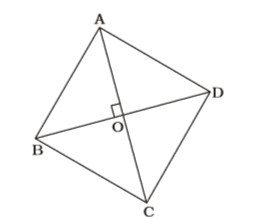
Area of rhombus = 1 d1d2 2 ⇒ 216 = 1 × 24 × d2 2 ⇒ d2 = 216 = 18 12
∴ AO = 12 cm, BO = 9 cm
⇒ AB = √24² + 10² = √576 + 100
= √225 = 15 cm
∴ Perimeter of rhombus = 4 × 15 = 60 cmCorrect Option: B
Using Rule 12,

Area of rhombus = 1 d1d2 2 ⇒ 216 = 1 × 24 × d2 2 ⇒ d2 = 216 = 18 12
∴ AO = 12 cm, BO = 9 cm
⇒ AB = √24² + 10² = √576 + 100
= √225 = 15 cm
∴ Perimeter of rhombus = 4 × 15 = 60 cm
- The sides of a quadrilateral are in the ratio 3 : 4 : 5 : 6 and its perimeter is 72 cm. The length of its greatest side (in cm) is
-
View Hint View Answer Discuss in Forum
3x + 4x + 5x + 6x = 72
⇒ 18x = 72
⇒ x = 4
∴ Largest side = 6x = 6 × 4 = 24 cm.Correct Option: A
3x + 4x + 5x + 6x = 72
⇒ 18x = 72
⇒ x = 4
∴ Largest side = 6x = 6 × 4 = 24 cm.
- Point O is the centre of a circle of radius 5 cm. At a distance of 13 cm from O, a point P is taken. From this point, two tangents PQ and PR are drawn to the circle. Then , the area of quadrilateral PQOR is
-
View Hint View Answer Discuss in Forum
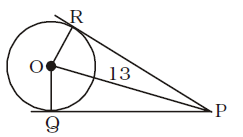
OQ ⊥ QP ; OR ⊥ PR
OR = OQ = radius
PQ = PR = Tangents from anexterior point
OP is common.
∴ ∆ORP ≅ ∆OPQ
In right ∆OPQ,
OP = 13 cm., OQ = 5 cm.
∴ PQ = √13² - 5² = √169 - 25
= √144 = 12 cm.Area of ∆OPQ = 1 × 12 × 5 = 30 sq. cm. 2
∴ Area of quadrilateral PQOR = 2 × 30 = 60 sq. cm.Correct Option: A

OQ ⊥ QP ; OR ⊥ PR
OR = OQ = radius
PQ = PR = Tangents from anexterior point
OP is common.
∴ ∆ORP ≅ ∆OPQ
In right ∆OPQ,
OP = 13 cm., OQ = 5 cm.
∴ PQ = √13² - 5² = √169 - 25
= √144 = 12 cm.Area of ∆OPQ = 1 × 12 × 5 = 30 sq. cm. 2
∴ Area of quadrilateral PQOR = 2 × 30 = 60 sq. cm.

