Point O is the centre of a circle of radius 5 cm. At a distance

Home » Aptitude » Mensuration » Question

Point O is the centre of a circle of radius 5 cm. At a distance of 13 cm from O, a point P is taken. From this point, two tangents PQ and PR are drawn to the circle. Then , the area of quadrilateral PQOR is

1. 60 cm.²
2. 32.5 cm.²
3. 65 cm.²
4. 30 cm.²

Correct Option: A

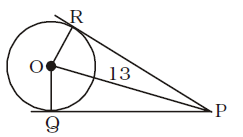
OQ ⊥ QP ; OR ⊥ PR
OR = OQ = radius
PQ = PR = Tangents from anexterior point
OP is common.
∴ ∆ORP ≅ ∆OPQ
In right ∆OPQ,
OP = 13 cm., OQ = 5 cm.
∴ PQ = √13² - 5² = √169 - 25
= √144 = 12 cm.

Area of ∆OPQ =	1	× 12 × 5 = 30 sq. cm.
	2

∴ Area of quadrilateral PQOR = 2 × 30 = 60 sq. cm.