Algebra
-
If x = √ √5 + 1 then the value of 5x2 – 5x – 1 is √5 − 1
-
View Hint View Answer Discuss in Forum
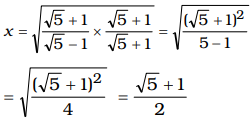
= 5 
(√5 + 1) 
2 − 5 (√5 + 1) − 1 2 2 = 5 
5 + 1 + 2√5 
− 5√5 + 5 − 1 4 2 = 5 
3 + √5 
− 5√5 + 5 − 1 2 2 = 15 + 5√5 − 5√5 − 5 − 2 2 = 8 = 4 2 Correct Option: C
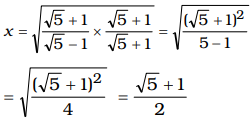
= 5 
(√5 + 1) 
2 − 5 (√5 + 1) − 1 2 2 = 5 
5 + 1 + 2√5 
− 5√5 + 5 − 1 4 2 = 5 
3 + √5 
− 5√5 + 5 − 1 2 2 = 15 + 5√5 − 5√5 − 5 − 2 2 = 8 = 4 2
-
If 2a + b = 3, then find the value of a + b a + 4b a + 2b
-
View Hint View Answer Discuss in Forum
2a + b = 3 (Given) a + 4b
⇒ 2a + b = 3a + 12b
⇒ 3a – 2a = b – 12 b
⇒ a = – 11bThen, a + b = − 11b + b a + 2b − 11b + 2b = −10b = 10 −9b 9 Correct Option: C
2a + b = 3 (Given) a + 4b
⇒ 2a + b = 3a + 12b
⇒ 3a – 2a = b – 12 b
⇒ a = – 11bThen, a + b = − 11b + b a + 2b − 11b + 2b = −10b = 10 −9b 9
- If a * b = 2 (a + b), then 5 * 2 is equal to :
-
View Hint View Answer Discuss in Forum
a * b = 2 (a + b)
∴ 5 * 2 = 2 (5 + 2)
= 2 × 7 = 14Correct Option: C
a * b = 2 (a + b)
∴ 5 * 2 = 2 (5 + 2)
= 2 × 7 = 14
-
1 + 1 x + 4
-
View Hint View Answer Discuss in Forum
Given expression
= 
1 + 1 

1 + 1 

1 + 1 

1 + 1 
x x + 1 x + 2 x + 3 = x + 1 × x + 2 × x + 3 × x + 4 x x + 1 x + 2 x + 3 = x + 4 x Correct Option: D
Given expression
= 
1 + 1 

1 + 1 

1 + 1 

1 + 1 
x x + 1 x + 2 x + 3 = x + 1 × x + 2 × x + 3 × x + 4 x x + 1 x + 2 x + 3 = x + 4 x
- Two numbers x and y (x > y) are such that their sum is equal to three times their difference.
Then value of 3xy will be: 2(x2 − y2)
-
View Hint View Answer Discuss in Forum
(x + y) = 3 (x – y) = 3x – 3y
⇒ 3y + y = 3x – x
⇒ 2x = 4y
⇒ x = 2y⇒ x = 2 y 1
∴ x = 2, y = 13xy = 3 × 2 × 1 = 6 = 1 2(x2 − y2) 2 × (4 − 1) 6 Correct Option: B
(x + y) = 3 (x – y) = 3x – 3y
⇒ 3y + y = 3x – x
⇒ 2x = 4y
⇒ x = 2y⇒ x = 2 y 1
∴ x = 2, y = 13xy = 3 × 2 × 1 = 6 = 1 2(x2 − y2) 2 × (4 − 1) 6

