Algebra
- If 22x – y = 16 and 2x + y = 32, the value of xy is
-
View Hint View Answer Discuss in Forum
22x – y = 16 = 24
⇒ 2x – y = 4 ............... (i)
2x + y = 32 = 25
⇒ x + y = 5 ............... (ii)
On adding equations (i) and (ii),
3x = 9 ⇒ x = 3
From equation (ii),
y = 5 – x = 5 – 3 = 2
∴ xy = 3 × 2 = 6Correct Option: C
22x – y = 16 = 24
⇒ 2x – y = 4 ............... (i)
2x + y = 32 = 25
⇒ x + y = 5 ............... (ii)
On adding equations (i) and (ii),
3x = 9 ⇒ x = 3
From equation (ii),
y = 5 – x = 5 – 3 = 2
∴ xy = 3 × 2 = 6
- The value of the expression x4 – 17x3 + 17x2 – 17x + 17 at x = 16 is
-
View Hint View Answer Discuss in Forum
x4 – 17x3 + 17x2 – 17x + 17
= x4 – 16x3 + 16x2 – 16x – x3 + x2 – x + 17
When x = 16,
Expression = 164 – 164 + 163 – 162 – 163 + 162 – 16 + 17 = 1Correct Option: B
x4 – 17x3 + 17x2 – 17x + 17
= x4 – 16x3 + 16x2 – 16x – x3 + x2 – x + 17
When x = 16,
Expression = 164 – 164 + 163 – 162 – 163 + 162 – 16 + 17 = 1
-
If 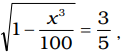
then x equals
-
View Hint View Answer Discuss in Forum
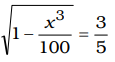
Squaring both sides,1 − x3 = 9 100 25 ⇒ x3 = 1 − 9 = 25 − 9 = 16 100 25 25 25 ⇒ x3 = 16 × 100 = 64 25
∴ 3√64 = 3√4 × 4 × 4 = 4Correct Option: B
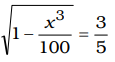
Squaring both sides,1 − x3 = 9 100 25 ⇒ x3 = 1 − 9 = 25 − 9 = 16 100 25 25 25 ⇒ x3 = 16 × 100 = 64 25
∴ 3√64 = 3√4 × 4 × 4 = 4
-
If a = c = e = 3,then 2a2 + 3c2 +4e2 = ? b d f 2b2 + 3d2 + 4f2
-
View Hint View Answer Discuss in Forum
a = c = e = 3 b d f
⇒ a = 3b ; c = 3d ; e = 3f∴ 2a2 + 3c2 +4e2 2b2 + 3d2 + 4f2 = 2 × 9b2 + 3 × 9d2 + 4 × 9f2 2b2 + 3d2 + 4f2 = 9(2b2 + 3d2 +4f2) = 9 2b2 + 3d2 + 4f2 Correct Option: D
a = c = e = 3 b d f
⇒ a = 3b ; c = 3d ; e = 3f∴ 2a2 + 3c2 +4e2 2b2 + 3d2 + 4f2 = 2 × 9b2 + 3 × 9d2 + 4 × 9f2 2b2 + 3d2 + 4f2 = 9(2b2 + 3d2 +4f2) = 9 2b2 + 3d2 + 4f2
- If a2x + 2 = 1, where a is a positive real number other than 1, then x is equal to
-
View Hint View Answer Discuss in Forum
We know that a° = 1
∴ a2x + 2 = 1 = a°
⇒ 2x +2 = 0⇒ x = − 2 = −1 2 Correct Option: B
We know that a° = 1
∴ a2x + 2 = 1 = a°
⇒ 2x +2 = 0⇒ x = − 2 = −1 2

