Mensuration
- The area of an isosceles triangle is 4 square unit. If the length of the third side is 2 unit, the length of each equal side is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
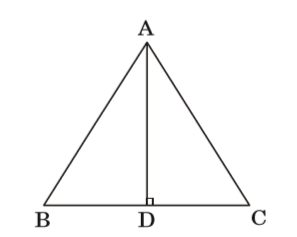
Let, AB = AC = x units
BD = DC = 1 unit [∵ BC = 2 units]
Now, AD = √AB² - BD²
= √x² - 1∴ 1 × BC × AD = 4 2 ⇒ 1 × 2 × √x² - 1 = 4 2
⇒ √x² - 1 = 4
⇒ x² – 1 = 16
⇒ x² = 17
⇒ x = √17unitsCorrect Option: C
Using Rule 1,

Let, AB = AC = x units
BD = DC = 1 unit [∵ BC = 2 units]
Now, AD = √AB² - BD²
= √x² - 1∴ 1 × BC × AD = 4 2 ⇒ 1 × 2 × √x² - 1 = 4 2
⇒ √x² - 1 = 4
⇒ x² – 1 = 16
⇒ x² = 17
⇒ x = √17units
- The ratio of sides of a triangle is 3:4:5 and area of the triangle is 72 square unit. Then the area of an equilateral triangle whose perimeter is same as that of the previous triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 6,
Sides of triangle
Let 3x, 4x and 5x units
Here, (3x)² + (4x)² = (5x)²
∴ It is a right angled triangle.
Now, Area of triangle= 1 × 3x × 4x = 6x² 2
∴ 6x² = 72⇒ x² = 72 6
⇒ x = 1√2 = 2√3
Perimeter of right angled triangle = 3x + 4x + 5x
= 12x = 12 × 2√3 =24√3 units
∴ Perimeter of equilateral triangle = 24√3 unitsIts side = 24√3 = 8√3 3 Area = √3 = × (side)² 4 = √3 = × 8√3 × 8√3 4
= 48√3 sq units.Correct Option: B
Using Rule 1 and 6,
Sides of triangle
Let 3x, 4x and 5x units
Here, (3x)² + (4x)² = (5x)²
∴ It is a right angled triangle.
Now, Area of triangle= 1 × 3x × 4x = 6x² 2
∴ 6x² = 72⇒ x² = 72 6
⇒ x = 1√2 = 2√3
Perimeter of right angled triangle = 3x + 4x + 5x
= 12x = 12 × 2√3 =24√3 units
∴ Perimeter of equilateral triangle = 24√3 unitsIts side = 24√3 = 8√3 3 Area = √3 = × (side)² 4 = √3 = × 8√3 × 8√3 4
= 48√3 sq units.
- A right angled isosceles triangle is inscribed in a semi-circle of radius 7 cm. The area enclosed by the semi-circle but exterior to the triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 14,
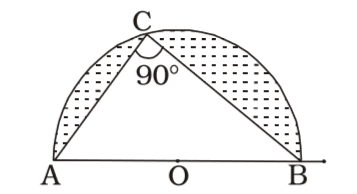
∠ACB = 90°
AC = CB = x cm
AB = 14 cm
From ∆ ABC
AC² + BC² = AB²
⇒ x² + x² = 142
⇒ 2x² = 14 × 14
⇒ x² = 14 × 7
⇒ x = √17 × 7 = 7√2cm
∴ Area of ∆ ABC= 1 × AC × BC 2 = 1 × 7√2 × 7√2 = 49 sq.cm. 2
Area of semi-circle= πr² = 22 × 7 × 7 2 7 × 2
= 77 sq. cm
∴ Area of the shaded region = 77 – 49 = 28 sq. cm
= 28 cm²Correct Option: B
Using Rule 1 and 14,

∠ACB = 90°
AC = CB = x cm
AB = 14 cm
From ∆ ABC
AC² + BC² = AB²
⇒ x² + x² = 142
⇒ 2x² = 14 × 14
⇒ x² = 14 × 7
⇒ x = √17 × 7 = 7√2cm
∴ Area of ∆ ABC= 1 × AC × BC 2 = 1 × 7√2 × 7√2 = 49 sq.cm. 2
Area of semi-circle= πr² = 22 × 7 × 7 2 7 × 2
= 77 sq. cm
∴ Area of the shaded region = 77 – 49 = 28 sq. cm
= 28 cm²
- The area (in sq. unit) of the triangle formed in the first quadrant by the line 3x + 4y = 12 is
-
View Hint View Answer Discuss in Forum
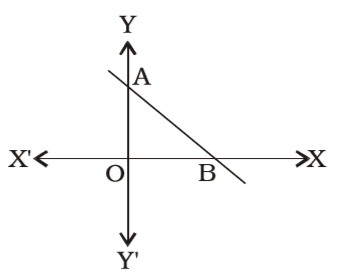
Putting y = 0 in the equation 3x + 4y = 12,
3x + 0 = 12 ⇒ x = 4
Co-ordinates of point B = (4, 0)
Putting x = 0 in the equation 3x + 4y = 12
0 + 4y = 12 ⇒ y = 3
∴ Co-ordinates of point A = (0, 3) ⇒ OB = 4 and OA = 3
∴ Area of ∆ OAB= 1 × OB × OA 2 = 1 × 4 × 3 = 6 sq.units 2 Correct Option: C

Putting y = 0 in the equation 3x + 4y = 12,
3x + 0 = 12 ⇒ x = 4
Co-ordinates of point B = (4, 0)
Putting x = 0 in the equation 3x + 4y = 12
0 + 4y = 12 ⇒ y = 3
∴ Co-ordinates of point A = (0, 3) ⇒ OB = 4 and OA = 3
∴ Area of ∆ OAB= 1 × OB × OA 2 = 1 × 4 × 3 = 6 sq.units 2
- The height of an equilateral triangle is 15 cm. The area of the triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 6,
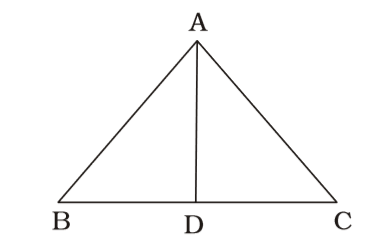
Let AB = BC = CA = 2a cm, AD ⊥ BC
AD = √AB² - BD²
= √4a² - a² = √3a
∴ √3a = 15
⇒ a = 5√3
∴ 2a = Side = 10√3cm
∴ Area of triangle= √3 × (10√3)² 4
= 75√3 sq. cm.Correct Option: C
Using Rule 6,

Let AB = BC = CA = 2a cm, AD ⊥ BC
AD = √AB² - BD²
= √4a² - a² = √3a
∴ √3a = 15
⇒ a = 5√3
∴ 2a = Side = 10√3cm
∴ Area of triangle= √3 × (10√3)² 4
= 75√3 sq. cm.

