Mensuration
- The circumference of a circle is 100 cm. The side of a square inscribed in the circle is
-
View Hint View Answer Discuss in Forum
Radius of the circle = 100 cm 2π
When a square is inscribed in the circle, diagonal of the square is equal to diameter of the circle.∴ Diagonal of square = 2 × 100 = 100 cm 2π π Side of square = Diagonal √2 = 100 = 50√2 cm √2π π Correct Option: B
Radius of the circle = 100 cm 2π
When a square is inscribed in the circle, diagonal of the square is equal to diameter of the circle.∴ Diagonal of square = 2 × 100 = 100 cm 2π π Side of square = Diagonal √2 = 100 = 50√2 cm √2π π
- A path of uniform width surrounds a circular park. The difference of internal and external circumference of this circular path is 132 metres. Its width is : (Take π = 22/7 )
-
View Hint View Answer Discuss in Forum
Let the internal radius of the park be r and the external radius (with the path) be R.
The difference between the internal and external circumferences is 132 m.
i.e. 2πR – 2πr = 132
⇒ 2π (R – r) = 132⇒ R – r = 132 = 132 × 7 = 21 2π 2 × 22
Hence, the width of path = 21 metresCorrect Option: C
Let the internal radius of the park be r and the external radius (with the path) be R.
The difference between the internal and external circumferences is 132 m.
i.e. 2πR – 2πr = 132
⇒ 2π (R – r) = 132⇒ R – r = 132 = 132 × 7 = 21 2π 2 × 22
Hence, the width of path = 21 metres
- The ratio of the outer and the inner perimeter of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is :
-
View Hint View Answer Discuss in Forum
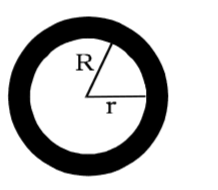
Let the shaded portion be the circular path.
Let the inner radius be r metres.
∴ Outer radius R = (r + 5) metres.
According to the question,2πR = 23 2πr 22 ⇒ R = 23 r 22 ⇒ r + 5 = 23 r 22
⇒ 23r = 22r + 110
⇒ r = 110 metres
∴ Diameter=2 × 110 = 220 metresCorrect Option: C

Let the shaded portion be the circular path.
Let the inner radius be r metres.
∴ Outer radius R = (r + 5) metres.
According to the question,2πR = 23 2πr 22 ⇒ R = 23 r 22 ⇒ r + 5 = 23 r 22
⇒ 23r = 22r + 110
⇒ r = 110 metres
∴ Diameter=2 × 110 = 220 metres
- The radius of the incircle of a triangle is 2 cm. If the area of the triangle is 6 cm², then its perimeter is
-
View Hint View Answer Discuss in Forum
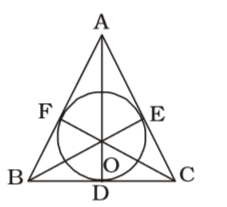
OD = OE = OF = 2cm.
∴ Area of ∆ABC
= Area of ∆AOB + Area of ∆BOC + Area of ∆AOC⇒ 6 = 1 × AB × 2 + 1 × BC × 2 + 1 × CA × 2 2 2 2
⇒ AB + BC + CA = 6 cmCorrect Option: C

OD = OE = OF = 2cm.
∴ Area of ∆ABC
= Area of ∆AOB + Area of ∆BOC + Area of ∆AOC⇒ 6 = 1 × AB × 2 + 1 × BC × 2 + 1 × CA × 2 2 2 2
⇒ AB + BC + CA = 6 cm
- The area of the circumcircle of an equilateral triangle is 3p sq. cm. The perimeter of the triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 18,
Circum-radius = Side √3 ∴ Area of circum-circle = π × Side² = 3π 3
⇒ Side² = 9
⇒ Side = 3 cm
∴ Perimeter of triangle = 3 + 3 + 3 = 9 cmCorrect Option: B
Using Rule 18,
Circum-radius = Side √3 ∴ Area of circum-circle = π × Side² = 3π 3
⇒ Side² = 9
⇒ Side = 3 cm
∴ Perimeter of triangle = 3 + 3 + 3 = 9 cm

