Mensuration
- The area of the incircle of an equilateral triangle of side 42 cm
is (Take π = 22/7) :
-
View Hint View Answer Discuss in Forum

Let ABC be the equilateral triangle of side 42 cm and let AD be perpendicular from A on BC.
Since the triangle is equilateral, so D bisects BC.
∴ BD = CD = 21 cm.
The centre of the inscribed circle will coincide with the centroid of ∆ ABC.Therefore, OD = 1 AD 3
In ∆ ABC
AB² = AD² + BD²
→ 42² = AD² + 21²
⇒ AD = √42² – 21²
= √(42 + 21)(42 - 21)
= √63 × 21 = 3 × 7√3cm∴ OD = 1 AD = × 7√3 3 = 22 × 7√3× 7√3 7
= 22 × 7 × 3 = 462 cm²Correct Option: B

Let ABC be the equilateral triangle of side 42 cm and let AD be perpendicular from A on BC.
Since the triangle is equilateral, so D bisects BC.
∴ BD = CD = 21 cm.
The centre of the inscribed circle will coincide with the centroid of ∆ ABC.Therefore, OD = 1 AD 3
In ∆ ABC
AB² = AD² + BD²
→ 42² = AD² + 21²
⇒ AD = √42² – 21²
= √(42 + 21)(42 - 21)
= √63 × 21 = 3 × 7√3cm∴ OD = 1 AD = × 7√3 3 = 22 × 7√3× 7√3 7
= 22 × 7 × 3 = 462 cm²
- The radii of two circles are 5cm and 12cm. The area of a third circle is equal to the sum of the area of the two circles. The radius of the third circle is :
-
View Hint View Answer Discuss in Forum
Using Rule 14,
πr² = π × 5² + π × 12²
⇒ r² = 25 + 144 = 169
⇒ r = √169 = 13 cmCorrect Option: A
Using Rule 14,
πr² = π × 5² + π × 12²
⇒ r² = 25 + 144 = 169
⇒ r = √169 = 13 cm
- The area of an equilateral triangle inscribed in a circle is 43 cm2. The area of the circle is
-
View Hint View Answer Discuss in Forum
Using Rule 6,
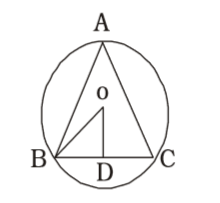
Area of ∆ABC = √3 × (side)² 4 ⇒ √3 × (side)² = 4√3 4
⇒ side = √16 = 4 cm
∴ ∠BOD = 60°⇒ sin 60° = BD OB ⇒ √3 = 2 ⇒ OB = 4 2 OB √3
∴ Area of circle = πr²= π × 16 = 16 π cm² 3 3 Correct Option: A
Using Rule 6,

Area of ∆ABC = √3 × (side)² 4 ⇒ √3 × (side)² = 4√3 4
⇒ side = √16 = 4 cm
∴ ∠BOD = 60°⇒ sin 60° = BD OB ⇒ √3 = 2 ⇒ OB = 4 2 OB √3
∴ Area of circle = πr²= π × 16 = 16 π cm² 3 3
- The area of the largest circle, that can be drawn inside a rectangle with sides 18 cm. by 14 cm, is
-
View Hint View Answer Discuss in Forum
Using Rule 14,

The largest circle will have radius equal to 7 cm.
∴ Area = π × r²= 22 × 7 × 7 = 154 cm² 7 Correct Option: B
Using Rule 14,

The largest circle will have radius equal to 7 cm.
∴ Area = π × r²= 22 × 7 × 7 = 154 cm² 7
- A circle is inscribed in an equilateral triangle of side 8 cm. The area of the portion between the triangle and the circle is
-
View Hint View Answer Discuss in Forum
Using Rule 6 and 14,

Radius of in-circle = BD cot 60°= 4 cm √3 Area of the circle = π × 4 × 4 √3 √3 = 16 π cm² = 16.76 cm² 3 Area of the triangle = √3 × 8 × 8 4
= 16√3 cm²
∴ Required area = 16√3 – 16.76
= (27.71 – 16.76) = 10.95 cm²Correct Option: B
Using Rule 6 and 14,

Radius of in-circle = BD cot 60°= 4 cm √3 Area of the circle = π × 4 × 4 √3 √3 = 16 π cm² = 16.76 cm² 3 Area of the triangle = √3 × 8 × 8 4
= 16√3 cm²
∴ Required area = 16√3 – 16.76
= (27.71 – 16.76) = 10.95 cm²

