Mensuration
- A solid brass sphere of radius 2.1 dm is converted into a right circular cylindrical rod of length 7 cm. The ratio of total surface areas of the rod to the sphere is
-
View Hint View Answer Discuss in Forum
Volume of copper sphere = 4 πr³ 3 = 4 π(21)³ cu.cm. 3
Volume of cylindrical rod = πR²H = πR² × 7 cu. cm.∴ πR² × 7 = 4 π × 21 × 21 × 21 3 ⇒ R² = 4 × 21 × 21 × 21 3 7
∴ R = √4 × 21 × 21
= 2 × 21 = 42 cm.
Surface area of sphere = 4πr² = 4π(21)² sq. cm.
Total surface area of the rod = 2πR(R + H) = 2π × 42 (42 + 7)
= 2π × 42 × 49 sq. cm.∴ Required ratio = 2π × 42 × 49 = 7 : 3 4π × 21 × 21 Correct Option: C
Volume of copper sphere = 4 πr³ 3 = 4 π(21)³ cu.cm. 3
Volume of cylindrical rod = πR²H = πR² × 7 cu. cm.∴ πR² × 7 = 4 π × 21 × 21 × 21 3 ⇒ R² = 4 × 21 × 21 × 21 3 7
∴ R = √4 × 21 × 21
= 2 × 21 = 42 cm.
Surface area of sphere = 4πr² = 4π(21)² sq. cm.
Total surface area of the rod = 2πR(R + H) = 2π × 42 (42 + 7)
= 2π × 42 × 49 sq. cm.∴ Required ratio = 2π × 42 × 49 = 7 : 3 4π × 21 × 21
- The radius of a cylindrical milk container is half its height and surface area of the inner part is 616 sq. cm. The amount of milk that the container can hold, approximately, is
[Use : √5 = 2.23 and π = 22/7]
-
View Hint View Answer Discuss in Forum
Surface area of milk pot. = 2πrh + πr² = πr(2h + r)
= πh 
2h + h 
= 5πrh² cu.cm. 2 2 4 ∴ 5 × 22 × h² = 616 4 7 ⇒ h² = 616 × 4 × 7 = 28 × 28 5 × 22 5
∴ Volume of milk = πr²h= 22 × h² × h 7 4 = 22 × 28 × 28 × 28 × h 28 5 × √5 = 22 × 28 × 28 × √5 × 22 × 28 × 28 × 2.23 × h 25 25
= 1538.5 cu. cm.
= 1.54 litres
= 1.53 litres (Approx.)Correct Option: B
Surface area of milk pot. = 2πrh + πr² = πr(2h + r)
= πh 
2h + h 
= 5πrh² cu.cm. 2 2 4 ∴ 5 × 22 × h² = 616 4 7 ⇒ h² = 616 × 4 × 7 = 28 × 28 5 × 22 5
∴ Volume of milk = πr²h= 22 × h² × h 7 4 = 22 × 28 × 28 × 28 × h 28 5 × √5 = 22 × 28 × 28 × √5 × 22 × 28 × 28 × 2.23 × h 25 25
= 1538.5 cu. cm.
= 1.54 litres
= 1.53 litres (Approx.)
- The height and the total surface area of a right circular cylinder are 4 cm and 8π sq.cm. respectively. The radius of the base of cylinder is
-
View Hint View Answer Discuss in Forum
Height of cylinder = 4 cm.
Total surface area = 2πr (r + h)
∴ 2πr (r + h) = 8π
⇒ r (r + 4) = 4
⇒ r² + 4r – 4 = 0⇒ r = - 4 ± √16 + 16 2 = - 4 ± √32 2
= – 2 + 2√2
because r ≠ –2 – 2√2
Note : If ax² + bx + c = 0, then x⇒ r = - b ± √b² - 4ac 2a Correct Option: A
Height of cylinder = 4 cm.
Total surface area = 2πr (r + h)
∴ 2πr (r + h) = 8π
⇒ r (r + 4) = 4
⇒ r² + 4r – 4 = 0⇒ r = - 4 ± √16 + 16 2 = - 4 ± √32 2
= – 2 + 2√2
because r ≠ –2 – 2√2
Note : If ax² + bx + c = 0, then x⇒ r = - b ± √b² - 4ac 2a
- If curved surface area of a cylinder is 1386 sq cm and height is 21 cm, what will be its radius? (Take π = 22/7)
-
View Hint View Answer Discuss in Forum
Curved surface area of cylinder = 2πrh
⇒ 2πrh = 1386⇒ 2 × 22 × r × 21 = 1386 7
⇒44 × 3 × r = 1386⇒ r = 1386 = 10.5 cm. 44 × 3 Correct Option: C
Curved surface area of cylinder = 2πrh
⇒ 2πrh = 1386⇒ 2 × 22 × r × 21 = 1386 7
⇒44 × 3 × r = 1386⇒ r = 1386 = 10.5 cm. 44 × 3
- A right circular conical structure stands on a circular base of 21 metre diameter and is 14 metre in height. The total cost of colour washing for its curved surface at Rs. 6 per square metre is (Take π = 22/7)
-
View Hint View Answer Discuss in Forum
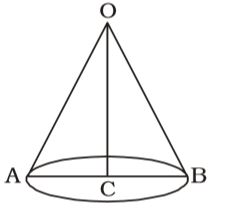
AC = 21 metres 2
OC = 14 metre
∴ Slant height (l) = √AC² + CO²= √ 
21 ² 
+ (14)² 2 = √ 441 + 196 4 = √ 441 + 784 = √ 1225 4 4 = 35 metre 2
∴ Curved surface area = πrl= 
22 × 21 × 35 
sq. metre 7 2 2
= 577.5 sq. metre
∴ Total expenditure on painting = Rs. (577.5 × 6) = Rs. 3465Correct Option: C

AC = 21 metres 2
OC = 14 metre
∴ Slant height (l) = √AC² + CO²= √ 
21 ² 
+ (14)² 2 = √ 441 + 196 4 = √ 441 + 784 = √ 1225 4 4 = 35 metre 2
∴ Curved surface area = πrl= 
22 × 21 × 35 
sq. metre 7 2 2
= 577.5 sq. metre
∴ Total expenditure on painting = Rs. (577.5 × 6) = Rs. 3465

