Mensuration
- If ∆ABC is similar to ∆DEF such that BC = 3 cm, EF = 4 cm and area of ∆ABC = 54 cm², then the area of ∆DEF is :
-
View Hint View Answer Discuss in Forum
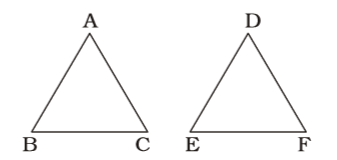
∆ABC ~ ∆DEF∴ ∆ABC = 3² ⇒ 54 = 9 ∆DEF 4² ∆DEF 16 ⇒ ∆DEF = 16 × 54 = 96 sq.cm. 9 Correct Option: C

∆ABC ~ ∆DEF∴ ∆ABC = 3² ⇒ 54 = 9 ∆DEF 4² ∆DEF 16 ⇒ ∆DEF = 16 × 54 = 96 sq.cm. 9
- The area of two similar triangles ABC and DEF are 20cm² and 45cm² respectively. If AB = 5 cm, then DE is equal to :
-
View Hint View Answer Discuss in Forum
∆ABC = AB² ∆DEF DE² ⇒ 20 = 25 45 DE² ⇒ DE² = 45 × 25 = 225 20 4 ∴ DE = 15 = 7.5 cm. 2 Correct Option: B
∆ABC = AB² ∆DEF DE² ⇒ 20 = 25 45 DE² ⇒ DE² = 45 × 25 = 225 20 4 ∴ DE = 15 = 7.5 cm. 2
- ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
-
View Hint View Answer Discuss in Forum
Join AC & DQ Q
∆APC and ∆BCP lie on the same base PC and between the same parallels AB and PC
∴ ar(∆APC) = ar(∆BCP)
Now, AD || CQ and AD = CQ ...(i)
∴ ADQC is a parallelogram.
Again ∆ADC and ∆DAQ are on the same base AD and between same parallels AD and CQ.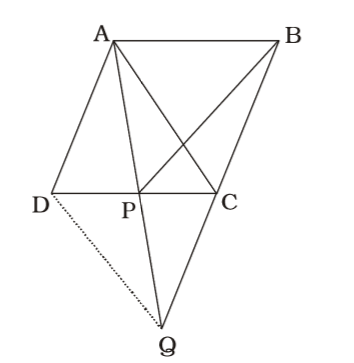
∴ ar(∆ADC) = ar(∆ADQ) Subtracting ar (DAP) from both sides, we get
ar(∆APC) = ar(∆DPQ) ...(ii)
From (i) and (ii),
we get ar(∆BPC) = ar(∆DPQ)Correct Option: A
Join AC & DQ Q
∆APC and ∆BCP lie on the same base PC and between the same parallels AB and PC
∴ ar(∆APC) = ar(∆BCP)
Now, AD || CQ and AD = CQ ...(i)
∴ ADQC is a parallelogram.
Again ∆ADC and ∆DAQ are on the same base AD and between same parallels AD and CQ.
∴ ar(∆ADC) = ar(∆ADQ) Subtracting ar (DAP) from both sides, we get
ar(∆APC) = ar(∆DPQ) ...(ii)
From (i) and (ii),
we get ar(∆BPC) = ar(∆DPQ)
- The ratio of the length of the parallel sides of a trapezium is 3:2. The shortest distance between them is 15 cm. If the area of the trapezium is 450 cm², the sum of the length of the parallel sides is
-
View Hint View Answer Discuss in Forum
Using Rule 13,
Area of the trapezium = 1/2 (sum of parallel sides) × altitude⇒ 450 = 1 (3x + 2x) × 15 2 ⇒ 5x = 450 × 2 = 60 cm 15 Correct Option: D
Using Rule 13,
Area of the trapezium = 1/2 (sum of parallel sides) × altitude⇒ 450 = 1 (3x + 2x) × 15 2 ⇒ 5x = 450 × 2 = 60 cm 15
- C1 and C2 are two concentric circles with centre at O. Their radii are 12 cm. and 3 cm. respectively. B and C are the point of contact of two tangents drawn to C2 from a point A lying on the circle C1. Then, the area of the quadrilateral ABOC is
-
View Hint View Answer Discuss in Forum
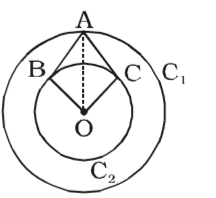
AB = AC = tangents from the same point
OB = OC = 3 cm
OA = 12 cm
∠ABO = 90°
∴ AB = √12² - 3²
= √15 × 9 = 3√15∆ OAB = 1 OB × AB 2 ∴ 1 × 3 × 3√15 = 9√15 2 2 ∴ Area of OABC = 9√15 sq.cm. 2 Correct Option: A

AB = AC = tangents from the same point
OB = OC = 3 cm
OA = 12 cm
∠ABO = 90°
∴ AB = √12² - 3²
= √15 × 9 = 3√15∆ OAB = 1 OB × AB 2 ∴ 1 × 3 × 3√15 = 9√15 2 2 ∴ Area of OABC = 9√15 sq.cm. 2

