76. If O is the centroid and AD, BE and CF are the three medians of ∆ABC with an area of 96 cm² then the area of ∆BOD in cm² is
    

1. 1. 8
      

   
   
   

   2. 12
      

   
   
   

   3. 16
      

   
   
   

   4. 24

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
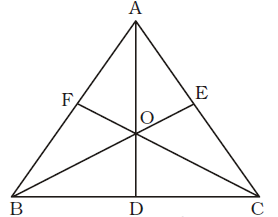
   Point O is the centroid of ∆ABC.
   ∴ ∆AOB ≡ ∆AOC ≡ ∆BOC
   Again, ∆BOD ≡ ∆COD
   

   ∴ Area of ∆BOD =	1	× Area of ∆ABC
   	6

   
   

   =	1	× 96 = 16 sq.cm.
   	6

   Correct Option: C

   
   Point O is the centroid of ∆ABC.
   ∴ ∆AOB ≡ ∆AOC ≡ ∆BOC
   Again, ∆BOD ≡ ∆COD
   

   ∴ Area of ∆BOD =	1	× Area of ∆ABC
   	6

   
   

   =	1	× 96 = 16 sq.cm.
   	6

---

77. In a triangle ABC, AB = 8 cm, AC = 10 cm and ÐB = 90°, then the area of ∆ABC is
    

1. 1. 49 sq.cm
      

   
   
   

   2. 36 sq.cm
      

   
   
   

   3. 25 sq.cm
      

   
   
   

   4. 24 sq.cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
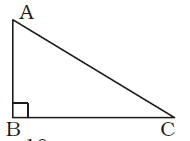
   AC = 10 cm.
   AB = 8 cm.
   ∴ BC = √AC² - AB²
   = √10² - 8² = √100 - 64
   = √36 = 6 cm.
   

   ∴ Area of ∆ABC =	1	× AB × BC
   	2

   
   

   ∴ Area of ∆ABC =	1	× 8 × 6 = 24 sq. cm.
   	2

   Correct Option: D

   
   AC = 10 cm.
   AB = 8 cm.
   ∴ BC = √AC² - AB²
   = √10² - 8² = √100 - 64
   = √36 = 6 cm.
   

   ∴ Area of ∆ABC =	1	× AB × BC
   	2

   
   

   ∴ Area of ∆ABC =	1	× 8 × 6 = 24 sq. cm.
   	2

---

---

78. In figure, DE || BC. If DE = 3 cm, BC = 6 cm and area of ∆ADE = 15 sq. cm, then the area of ∆ABC is
    
    

1. 1. 75 sq. cm.
      

   
   
   

   2. 45 sq. cm.
      

   
   
   

   3. 30 sq. cm.
      

   
   
   

   4. 60 sq. cm.

   
   
   

---

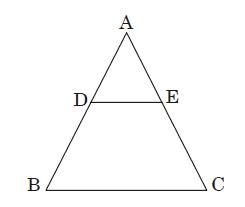
1. View Hint View Answer Discuss in Forum

   
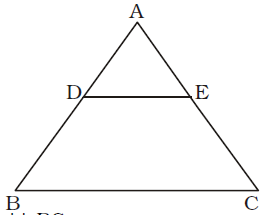
   DE || BC
   ∴ ∠ADE = ∠ABC
   ∠AED = ∠ACB
   By AA–similarity,
   ∆ADE ~ ∆ABC
   

   ∴	Area of ∆ABC	=	BC²
   	Area of ∆ADE		DE²

   
   

   ⇒	Area of ∆ABC	=	6²
   	15		3²

   
   

   =	36	= 4
   	9

   
   ∴ Area of DABC = 4 × 15
   = 60 sq. cm.

   Correct Option: D

   
   DE || BC
   ∴ ∠ADE = ∠ABC
   ∠AED = ∠ACB
   By AA–similarity,
   ∆ADE ~ ∆ABC
   

   ∴	Area of ∆ABC	=	BC²
   	Area of ∆ADE		DE²

   
   

   ⇒	Area of ∆ABC	=	6²
   	15		3²

   
   

   =	36	= 4
   	9

   
   ∴ Area of DABC = 4 × 15
   = 60 sq. cm.

---

79. ∆ABC is a right angled triangle, the radius of its circumcircle is 3 cm and the length of its altitude drawn from the opposite vertex to the hypotenuse is 2 cm. Then the area of the triangle is
    

1. 1. 12 sq. cm.
      

   
   
   

   2. 3 sq. cm.
      

   
   
   

   3. 6 sq. cm.
      

   
   
   

   4. 5 sq. cm.

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
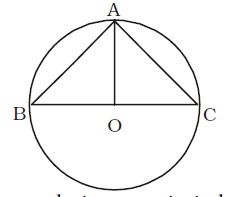
   The angle in a semi–circle is a right angle.
   ∴ BC = 2 × 3 = 6 cm.
   OA = 2 cm.
   

   ∴ Area of ∆ABC =	1	× BC × OA
   	2

   
   

   =	1	× 6 × 2 = 6 sq.cm.
   	2

   Correct Option: C

   
   The angle in a semi–circle is a right angle.
   ∴ BC = 2 × 3 = 6 cm.
   OA = 2 cm.
   

   ∴ Area of ∆ABC =	1	× BC × OA
   	2

   
   

   =	1	× 6 × 2 = 6 sq.cm.
   	2

---

---

80. The lengths of the diagonals of a rhombus are 8 cm and 6 cm. The area of rhombus is :
    

1. 1. 96 cm&su2;
      

   
   
   

   2. 60 cm&su2;
      

   
   
   

   3. 48 cm&su2;
      

   
   
   

   4. 24 cm&su2;

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Area of the rhombus
   

   ∴ Area of ∆ABC =	1	× d1 × d2
   	2

   
   

   =		1	× 8 × 6		sq. cm. = 24 sq.cm.
   		2

   Correct Option: D

   Area of the rhombus
   

   ∴ Area of ∆ABC =	1	× d1 × d2
   	2

   
   

   =		1	× 8 × 6		sq. cm. = 24 sq.cm.
   		2

---