Mensuration
- A cone of height 15 cm and basediameter 30 cm is carved out of a wooden sphere of radius 15 cm. The percentage of wasted wood is :
-
View Hint View Answer Discuss in Forum
Volume of the cone = 1 πr²h = 1 π(15)² × 15 3 3 = 1 π × (15)³ cm³. 3 Volume of the wooden sphere = 4 πr³ = 4 π(15)³ cm³ 3 3 Wasted wood = 4 π × (15)³ - 1 π(15)³ = π (15)³ cm³ 3 3 ∴ Required percentage = π × (15)³ × 100 = 75% 4 π(15)³ 3 Correct Option: A
Volume of the cone = 1 πr²h = 1 π(15)² × 15 3 3 = 1 π × (15)³ cm³. 3 Volume of the wooden sphere = 4 πr³ = 4 π(15)³ cm³ 3 3 Wasted wood = 4 π × (15)³ - 1 π(15)³ = π (15)³ cm³ 3 3 ∴ Required percentage = π × (15)³ × 100 = 75% 4 π(15)³ 3
- In a right circular cone, the radius of its base is 7 cm and its height 24 cm. A cross-section is made through the midpoint of the height parallel to the base. The volume of the upper portion is
-
View Hint View Answer Discuss in Forum
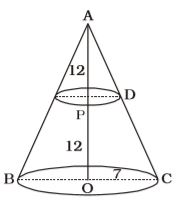
In ∆APD and ∆AOCAP = PD [∵ ∆APD ≅ ∆AOC] AO OC PD = AP × OC = 12 × 7 = 3.5 cm AO 24 ∴ Volume = 1 πr² × h 3 = 1 × 22 × 3.5 × 3.5 × 12 3 7
= 154 cm³Correct Option: B

In ∆APD and ∆AOCAP = PD [∵ ∆APD ≅ ∆AOC] AO OC PD = AP × OC = 12 × 7 = 3.5 cm AO 24 ∴ Volume = 1 πr² × h 3 = 1 × 22 × 3.5 × 3.5 × 12 3 7
= 154 cm³
- If the area of the base of a cone is 770 cm² and the area of the curved surface is 814 cm², then its volume (in cm³) is :
-
View Hint View Answer Discuss in Forum
Area of the base of cone = 770 cm²
⇒ r² = 770⇒ 22 r = 770 7 ⇒ r² = 770 × 7 = 245 22
∴ r = √245 = 7√5 cm
Curved surface area of the cone = πrl = 814⇒ r = 22 × 7√5 × l = 814 7 ⇒ l = 814 = 37 cm. 22 × √5 √5
Let the height of the cone be h cm, then h² + r² = l²⇒ h² + (7√5)² = 
37 
² √5 ⇒ h² + 245 = 1369 5 ⇒ h² = 1369 - 245 5 ⇒ h² = 1269 - 1225 = 144 5 5 ⇒ h = 12 cm √5 ∴ Volume of the cone = 1 πr²h 3 = 1 × 22 × 7√5 × 7√5 × 12 3 7 √5
= 616√5 cm&Sup3;Correct Option: D
Area of the base of cone = 770 cm²
⇒ r² = 770⇒ 22 r = 770 7 ⇒ r² = 770 × 7 = 245 22
∴ r = √245 = 7√5 cm
Curved surface area of the cone = πrl = 814⇒ r = 22 × 7√5 × l = 814 7 ⇒ l = 814 = 37 cm. 22 × √5 √5
Let the height of the cone be h cm, then h² + r² = l²⇒ h² + (7√5)² = 
37 
² √5 ⇒ h² + 245 = 1369 5 ⇒ h² = 1369 - 245 5 ⇒ h² = 1269 - 1225 = 144 5 5 ⇒ h = 12 cm √5 ∴ Volume of the cone = 1 πr²h 3 = 1 × 22 × 7√5 × 7√5 × 12 3 7 √5
= 616√5 cm&Sup3;
- Volume of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5. The ratio of their height is
-
View Hint View Answer Discuss in Forum
Let the height of the cones be h1 and h2 respectively.
∴ 1 πr1²h1 = 3 1 1 πr2²h2 4 3
(r1 and r2 are radii)= h1 = 1 × r2² = 1 × 25 = 25 h2 4 r1² 4 16 64
⇒ 25 : 64Correct Option: D
Let the height of the cones be h1 and h2 respectively.
∴ 1 πr1²h1 = 3 1 1 πr2²h2 4 3
(r1 and r2 are radii)= h1 = 1 × r2² = 1 × 25 = 25 h2 4 r1² 4 16 64
⇒ 25 : 64
- The height of the cone is 30 cm. A small cone is cut off at the top by a plane parallel to its base. If its volume is 1/27 of the volume of the cone, at what height, above the base, is the section made?
-
View Hint View Answer Discuss in Forum
Let H and R be the height and radius of bigger cone respectively and h and r that of smaller cone.
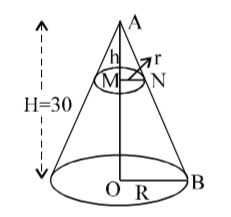
From triangles AOB and AMN. ∠A is common and MN || OB.
∴ Triangles AOB and AMN are similar,∴ AO = BO AM MN ⇒ 30 = R .........(i) h r ∴ Volume = 1 πr² × h 3 Volume of bigger cone = 1 πR²H 3
According to the question,1 πr²h = 
1 πR²H 
× 1 3 3 27 ⇒ r²h = R²H ⇒ 27r²h = R²H 27 ⇒ 27h = R² H r² ⇒ 27h = 
30 
² From(i) H h ⇒ 27h = 900 H r²
⇒ 27h³ = 900H = 900 × 30h³ = 900 × 30 = 1000 27
⇒ h = 3√1000 = 10 cm
∴ Required height = 30 – 10 = 20 cmCorrect Option: D
Let H and R be the height and radius of bigger cone respectively and h and r that of smaller cone.

From triangles AOB and AMN. ∠A is common and MN || OB.
∴ Triangles AOB and AMN are similar,∴ AO = BO AM MN ⇒ 30 = R .........(i) h r ∴ Volume = 1 πr² × h 3 Volume of bigger cone = 1 πR²H 3
According to the question,1 πr²h = 
1 πR²H 
× 1 3 3 27 ⇒ r²h = R²H ⇒ 27r²h = R²H 27 ⇒ 27h = R² H r² ⇒ 27h = 
30 
² From(i) H h ⇒ 27h = 900 H r²
⇒ 27h³ = 900H = 900 × 30h³ = 900 × 30 = 1000 27
⇒ h = 3√1000 = 10 cm
∴ Required height = 30 – 10 = 20 cm

