Mensuration
- A plate on square base made of brass is of length x cm and width 1 mm. The plate weighs 4725 gm. If 1 cubic cm of brass weighs 8.4 gram, then the value of x is :
-
View Hint View Answer Discuss in Forum
Volume of the plate of square base = Area of base × height
= x² × 1 = x² cu.cm. 10 10
According to the question,x² × 8.4 = 4725 10 ⇒ x² = 4725 × 10 = 5625 8.4
⇒ x = √5625 = 75 cm.Correct Option: A
Volume of the plate of square base = Area of base × height
= x² × 1 = x² cu.cm. 10 10
According to the question,x² × 8.4 = 4725 10 ⇒ x² = 4725 × 10 = 5625 8.4
⇒ x = √5625 = 75 cm.
- The length of the diagonal of a rectangle with sides 4 m and 3 m would be
-
View Hint View Answer Discuss in Forum

BD = √BC² + CD²
= √4² + 3² = √16 + 9 = √25 = 5 metreCorrect Option: C

BD = √BC² + CD²
= √4² + 3² = √16 + 9 = √25 = 5 metre
- In a right angled triangle ∆PQR, PR is the hypotenuse of length 20 cm, ∠PRQ = 30°, the area of the triangle is
-
View Hint View Answer Discuss in Forum
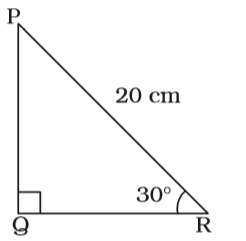
sin 30° = PQ PR ⇒ 1 = PQ 2 20 ⇒ PQ = 20 × 1 = 10 cm. 2 cos 30° = QR PR ⇒ √3 = QR 2 20 ⇒ QR = √3 × 20 = 10√3 cm. 2
∴ Area of triangle PQR= 1 × 10 × 10√3 2
= 50√3 square cm.Correct Option: A

sin 30° = PQ PR ⇒ 1 = PQ 2 20 ⇒ PQ = 20 × 1 = 10 cm. 2 cos 30° = QR PR ⇒ √3 = QR 2 20 ⇒ QR = √3 × 20 = 10√3 cm. 2
∴ Area of triangle PQR= 1 × 10 × 10√3 2
= 50√3 square cm.
- The perimeter of an equilateral triangle is equal to the circumference of a circle. The ratio of their areas is (Use π = 22/7)
-
View Hint View Answer Discuss in Forum
Using Rule 6,
Side of the equilateral triangle = x units (let)
According to the question, 3x = 2πr⇒ x = 2 πr 3
∴ Area of equilateral triangle= √3 × side² 4 = √3 × 
2 πr 
² 4 3 = √3 × 4 π² r² 4 9 = π² r² sq. units 3√3 ∴ Required ratio = π² r² : π r² 3√3
= π = 3√3= 22 : 3√3 = 22 : 21√3 7 Correct Option: A
Using Rule 6,
Side of the equilateral triangle = x units (let)
According to the question, 3x = 2πr⇒ x = 2 πr 3
∴ Area of equilateral triangle= √3 × side² 4 = √3 × 
2 πr 
² 4 3 = √3 × 4 π² r² 4 9 = π² r² sq. units 3√3 ∴ Required ratio = π² r² : π r² 3√3
= π = 3√3= 22 : 3√3 = 22 : 21√3 7
- From any point inside an equilateral triangle, the lengths of perpendiculars on the sides are ‘a’ cm, ‘b’ cm and ‘c’ cms. Its area (in cm2) is
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 6,
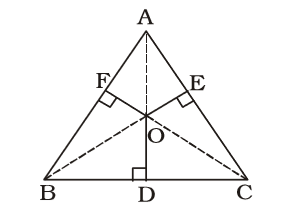
OD = a cm., OE = b cm.
OF = c cm.
BC = AC = AB
Area of ∆ABC = Area of (∆BOC + ∆COE + ∆BOA)= 1 × BC × a + 1 AC × b + 1 × AB × c 2 2 2 = 1 BC(a + b + c)..........(i) 2
(∵ AB = BC = CA)
Again, Area of ∆ABC= √3 × BC² 4 ∴ √3 × BC² = 1 BC(a + b + c) 4 2 ⇒ BC = 2 (a + b + c) √3
[From equation (i)]∴ Required area = 1 × 2 (a + b + c)² 2 √3 = √3 (a + b + c) √3 × √3 = √3 (a + b + c) sq. units. 3 Correct Option: B
Using Rule 1 and 6,

OD = a cm., OE = b cm.
OF = c cm.
BC = AC = AB
Area of ∆ABC = Area of (∆BOC + ∆COE + ∆BOA)= 1 × BC × a + 1 AC × b + 1 × AB × c 2 2 2 = 1 BC(a + b + c)..........(i) 2
(∵ AB = BC = CA)
Again, Area of ∆ABC= √3 × BC² 4 ∴ √3 × BC² = 1 BC(a + b + c) 4 2 ⇒ BC = 2 (a + b + c) √3
[From equation (i)]∴ Required area = 1 × 2 (a + b + c)² 2 √3 = √3 (a + b + c) √3 × √3 = √3 (a + b + c) sq. units. 3
-
-