Mensuration
- From a point P which is at a distance of 13 cm from centre O of a circle of radius 5 cm, in the same plane, a pair of tangentsPQ and PR are drawn to the circle. Area of quadrilateral PQOR is
-
View Hint View Answer Discuss in Forum
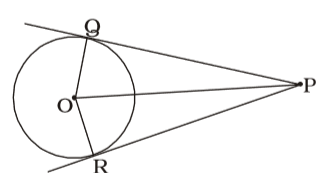
∠OQP = ∠ORP = 90°
PQ = √OP² - OQ²
= √13⊃ - 5⊃ = 12
∴ Area of PQOR = 2 × ∆OPQ= 2 × 1 × 5 × 12 2
= 60 sq. cmCorrect Option: B

∠OQP = ∠ORP = 90°
PQ = √OP² - OQ²
= √13⊃ - 5⊃ = 12
∴ Area of PQOR = 2 × ∆OPQ= 2 × 1 × 5 × 12 2
= 60 sq. cm
- In ∆ ABC, O is the centroid and AD, BE, CF are three medians and the area of ∆AOE = 15 cm², then area of quadrilateral BDOFis
-
View Hint View Answer Discuss in Forum
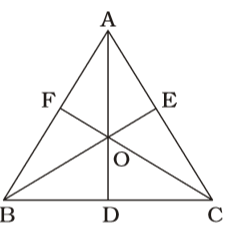
ar(∆AOE) = ar(∆BOD) = ar(∆BOF)
Area of quadrilateral BDOF = 2 × 15 = 30 sq.cm.Correct Option: B

ar(∆AOE) = ar(∆BOD) = ar(∆BOF)
Area of quadrilateral BDOF = 2 × 15 = 30 sq.cm.
- The in-radius of a triangle is 6 cm, and the sum of the lengths of its sides is 50 cm. The area of the triangle (in square cm.) is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
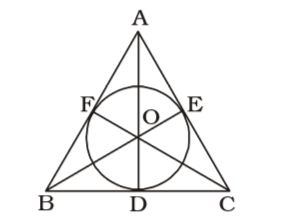
OD = OE = OF = 6 cm.
Area of triangle ABC = Area of (∆AOB + ∆BOC + ∆AOC)= 1 AB × OF + = 1 BC × OD + = 1 AC × DE 2 2 2 = 1 × 6 (AB + BC + CA) 2 = 1 × 6 × 50 = 150 square cm. 2 Correct Option: A
Using Rule 1,

OD = OE = OF = 6 cm.
Area of triangle ABC = Area of (∆AOB + ∆BOC + ∆AOC)= 1 AB × OF + = 1 BC × OD + = 1 AC × DE 2 2 2 = 1 × 6 (AB + BC + CA) 2 = 1 × 6 × 50 = 150 square cm. 2
- Three circles of radii 4 cm, 6 cm and 8 cm touch each other pairwise externally. The area of the triangle formed, by the line-segments joining-the centres of the three circles is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
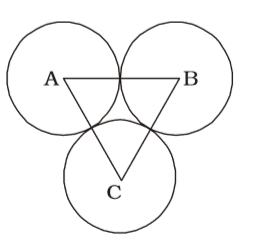
AB = 4 + 6 = 10 cm
BC = 6 + 8 = 14 cm
CA = 8 + 4 = 12 cm∴ Semi-perimeter = 10 + 14 + 12 = 18 cm 2
Area = √s(s - a)(s - b)(S - c)
= √18(18 - 10)(18 - 14)(18 - 12)
= √18 × 8 × 4 × 6
= 3 × 2 × 2 × 2√6
= 24√6 sq.cm.Correct Option: D
Using Rule 1,

AB = 4 + 6 = 10 cm
BC = 6 + 8 = 14 cm
CA = 8 + 4 = 12 cm∴ Semi-perimeter = 10 + 14 + 12 = 18 cm 2
Area = √s(s - a)(s - b)(S - c)
= √18(18 - 10)(18 - 14)(18 - 12)
= √18 × 8 × 4 × 6
= 3 × 2 × 2 × 2√6
= 24√6 sq.cm.
- Two circles with centre A and B and radius 2 units touch each other externally at ‘C’. A third circle with centre ‘C’ and radius ‘2’ units meets other two at D and E. Then the area of the quadrilateral ABDE is
-
View Hint View Answer Discuss in Forum
Using Rule 13,
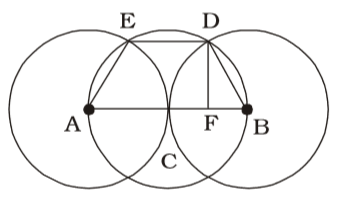
ABDE will be a trapezium AB = 4 units
DE = 1/2 AB = 2 units
FB = 1 unit, BD = 2 units.
∴ DF = √2² - 1²
= √3 units
∴ Area of ABDE= 1 (AB + DE) × DF 2 = 1 (4 + 2) × √3 2
= 3√3 sq. unitsCorrect Option: B
Using Rule 13,

ABDE will be a trapezium AB = 4 units
DE = 1/2 AB = 2 units
FB = 1 unit, BD = 2 units.
∴ DF = √2² - 1²
= √3 units
∴ Area of ABDE= 1 (AB + DE) × DF 2 = 1 (4 + 2) × √3 2
= 3√3 sq. units

