Mensuration

Mensuration

Easy Questions
Moderate Questions
Difficult Questions

Aptitude

Simplification
Number System
Fractions
Elementary Algebra
LCM and HCF
Approximation
Unitary Method
Linear Equation
Quadratic Equation
Discount
Average
Surds and Indices
Percentage
Square root and cube root
Order of Magnitude
Work and Wages
Odd Man Out and Series
Algebra
Profit and Loss
Stocks and Shares
True Discount
Ratio, Proportion
Partnership
Alligation or Mixture
Time and Work
Pipes and Cistern
Speed, Time and Distance
Problem on Trains
Height and Distance
Banker's Discount
Boats and Streams
Races and games
Problems on Ages
Clocks and Calendars
Simple interest
Compound Interest
Sets and Functions
Area and Perimeter
Volume and Surface Area of Solid Figures
Sequences and Series
Plane Geometry
Logarithm
Probability
Permutation and Combination
Statistics
Mensuration
Trigonometry
Aptitude miscellaneous
  1. The perimeter and length of a rectangle are 40 m and 12 m respectively. Its breadth will be








  1. View Hint View Answer Discuss in Forum

    Using Rule 9,
    Perimeter of rectangle = 40 metre
    Length = 12 metre
    ∴ 2(l + b) = 40
    ⇒ 2 (12 + b) = 40

    ⇒ 12 + b =
    40
    		 = 20
    2

    ⇒ b = 20 – 12 = 8 metre

    Correct Option: B

    Using Rule 9,
    Perimeter of rectangle = 40 metre
    Length = 12 metre
    ∴ 2(l + b) = 40
    ⇒ 2 (12 + b) = 40

    ⇒ 12 + b =
    40
    		 = 20
    2

    ⇒ b = 20 – 12 = 8 metre

  1. If the perimeter of a square and a rectangle are the same, then the area P and Q enclosed by them would satisfy the condition








  1. View Hint View Answer Discuss in Forum

    Using Rule 10,
    Let the side of square be 1 cm, then 2 (l + b)
    = 4 × side = 4 × 1
    ⇒ l + b = 2, If l = 1.5, b = 0.5
    ∴ Area of square = 1 sq.cm.
    and Area of rectangle = 1.5 × 0.5 = 0.75 sq.cm.
    For a given perimeter, square has the largest area. i.e, P > Q

    Correct Option: C

    Using Rule 10,
    Let the side of square be 1 cm, then 2 (l + b)
    = 4 × side = 4 × 1
    ⇒ l + b = 2, If l = 1.5, b = 0.5
    ∴ Area of square = 1 sq.cm.
    and Area of rectangle = 1.5 × 0.5 = 0.75 sq.cm.
    For a given perimeter, square has the largest area. i.e, P > Q

  1. PQRS is a square with side 10 cm. A, B, C and D are mid–points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is








  1. View Hint View Answer Discuss in Forum


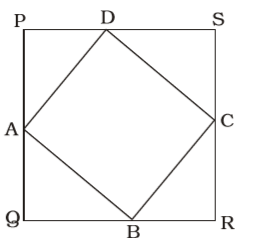
    PA = AQ = QB = 5 cm.
    ∴ ∠AQB = 90°
    ∴ AB = √AQ² + QB²
    = √5² + 5² = √25 + 25
    = √50 = 5√2 cm.
    ∴ Perimeter of ABCD = 4 × 5√2 = 20√2 cm.

    Correct Option: B


    PA = AQ = QB = 5 cm.
    ∴ ∠AQB = 90°
    ∴ AB = √AQ² + QB²
    = √5² + 5² = √25 + 25
    = √50 = 5√2 cm.
    ∴ Perimeter of ABCD = 4 × 5√2 = 20√2 cm.

  1. A piece of wire when bent to form a circle will have a radius of 84 cm. If the wire is bent to form a square, the length of a side of the square is








  1. View Hint View Answer Discuss in Forum

    Using Rule 14,
    Length of wire = Circumference of circle = 2πr

    = 2 ×
    22
    		 × 84 = 528 cm.
    2

    ∴ Perimeter of square = 528 cm.
    ⇒ 4 × side = 528
    ⇒ Side =
    528
    		 = 132 cm.
    4

    Correct Option: B

    Using Rule 14,
    Length of wire = Circumference of circle = 2πr

    = 2 ×
    22
    		 × 84 = 528 cm.
    2

    ∴ Perimeter of square = 528 cm.
    ⇒ 4 × side = 528
    ⇒ Side =
    528
    		 = 132 cm.
    4

  1. The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 9 cm. Determine the corresponding side of the second triangle.








  1. View Hint View Answer Discuss in Forum

    If the required side be x cm, then

    30
    		 =
    9
    20x

    ⇒ 3x = 9 × 2
    ⇒ x =
    9 × 2
    		 = 6 cm.
    3

    Correct Option: B

    If the required side be x cm, then

    30
    		 =
    9
    20x

    ⇒ 3x = 9 × 2
    ⇒ x =
    9 × 2
    		 = 6 cm.
    3