Mensuration
- If the lengths of the sides AB, BC and CA of a triangle ABC are 10 cm, 8 cm and 6 cm respectively and if M is the mid - point of BC and MN || AB to cut AC at N, then the area of the trapezium ABMN is equal to
-
View Hint View Answer Discuss in Forum
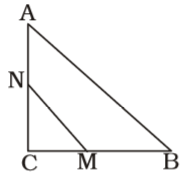
∵ 8² + 6² = 10²
∴ ∆ABC is a right angled triangle. CM = MB = 4 cm.
N is the mid point of AC.
∴ CN = 3 cm.
∴ Area of trapezium ABMN
= Area of ∆ABC – Area of ∆CMN= 1 × 6 × 8 - 1 × 3 × 4 2 2
= 24 – 6 = 18 sq. cm.Correct Option: A

∵ 8² + 6² = 10²
∴ ∆ABC is a right angled triangle. CM = MB = 4 cm.
N is the mid point of AC.
∴ CN = 3 cm.
∴ Area of trapezium ABMN
= Area of ∆ABC – Area of ∆CMN= 1 × 6 × 8 - 1 × 3 × 4 2 2
= 24 – 6 = 18 sq. cm.
- The external fencing of a circular path around a circular plot of land is 33 m more than its interior fencing. The width of the path around the plot is
-
View Hint View Answer Discuss in Forum
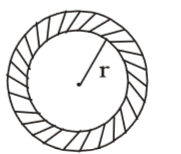
In-radius of circular plot = r metre (let)
Width of path = x metre
∴ Ex radius = (r + x) metre
According to the question 2π (r + x) – 2πr = 33
⇒ 2πr + 2πx – 2πr = 33
⇒ 2πx = 33= 2 × 22 × x = 33 7 ⇒ x = 33 × 7 = 21 metre 2 × 22 4
= 5.25 metreCorrect Option: B

In-radius of circular plot = r metre (let)
Width of path = x metre
∴ Ex radius = (r + x) metre
According to the question 2π (r + x) – 2πr = 33
⇒ 2πr + 2πx – 2πr = 33
⇒ 2πx = 33= 2 × 22 × x = 33 7 ⇒ x = 33 × 7 = 21 metre 2 × 22 4
= 5.25 metre
- The sides of a rhombus are 10 cm each and a diagonal measures 16 cm. Area of the rhombus is
-
View Hint View Answer Discuss in Forum
Using Rule 12,
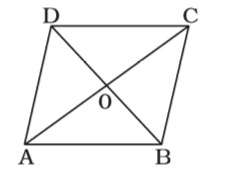
AB = BC = CD = DA = 10 cm
AC = 16 cm
In ∆OAB OA = 8 cm
AB = 10 cm
∠AOB = 90°
∴ OB = √AB² - OA²
= √10² - 8²
= √(10 + 8)(10 - 8)
= √18 × 2 = √36
= 6 cm
∴ BD = 2 × OB = 2 × 6 = 12 cm
∴ Area of rhombus ABCD= 1 d1 × d2 2 = 1 × 16 × 12 = 96 sq. cm. 2 Correct Option: A
Using Rule 12,

AB = BC = CD = DA = 10 cm
AC = 16 cm
In ∆OAB OA = 8 cm
AB = 10 cm
∠AOB = 90°
∴ OB = √AB² - OA²
= √10² - 8²
= √(10 + 8)(10 - 8)
= √18 × 2 = √36
= 6 cm
∴ BD = 2 × OB = 2 × 6 = 12 cm
∴ Area of rhombus ABCD= 1 d1 × d2 2 = 1 × 16 × 12 = 96 sq. cm. 2
- The perimeter of a triangle is 54 m and its sides are in the ratio of 5 : 6 : 7. The area of the triangleis
-
View Hint View Answer Discuss in Forum
Using Rule 1,
Ratio of the lengths of sides = 5 : 6 : 7
Sum of ratios = 5 + 6 + 7 = 18⇒ Sides ⇒ 5 × 54 = 15 metre 18 6 × 54 = 18 metre 18 7 × 54 = 21 metre 18 Semi-perimeter (s) = 15 + 18 + 21 = 54 = 27 2 2
∴ Area of triangle = √s(s - a)(s - b)(s - c)
= √27(27 - 15)(27 - 18)(27 - 21)
= √27 × 12 × 9 7times; 6
= √3 × 3 × 3 × 2 × 2 × 3 × 3 × 3 × 2 × 3 = 3 × 3 × 3 × 2 6 =
= 3 × 3 × 3 × 2√6
= 54√6 sq.metreCorrect Option: B
Using Rule 1,
Ratio of the lengths of sides = 5 : 6 : 7
Sum of ratios = 5 + 6 + 7 = 18⇒ Sides ⇒ 5 × 54 = 15 metre 18 6 × 54 = 18 metre 18 7 × 54 = 21 metre 18 Semi-perimeter (s) = 15 + 18 + 21 = 54 = 27 2 2
∴ Area of triangle = √s(s - a)(s - b)(s - c)
= √27(27 - 15)(27 - 18)(27 - 21)
= √27 × 12 × 9 7times; 6
= √3 × 3 × 3 × 2 × 2 × 3 × 3 × 3 × 2 × 3 = 3 × 3 × 3 × 2 6 =
= 3 × 3 × 3 × 2√6
= 54√6 sq.metre
- The lengths of two parallel sides of a trapezium are 6 cm and 8 cm. If the height of the trapezium be 4 cm, then its area is
-
View Hint View Answer Discuss in Forum
Using Rule 13,
Area of trapezium= 1 (sum of parallel sides) × per-pendicular distance 2 = 1 (6 + 8) × 4 = 1 × 14 × 4 2 2
= 28 sq. cm.Correct Option: B
Using Rule 13,
Area of trapezium= 1 (sum of parallel sides) × per-pendicular distance 2 = 1 (6 + 8) × 4 = 1 × 14 × 4 2 2
= 28 sq. cm.

