Mensuration
- On increasing each side of a square by 50%, the ratio of the area of new square formed and the given square will be
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Side of the given square = x cm (let)Side of new square = 3x cm. (let) 2 ∴ Required ratio of areas = 
3x 
² : x² = 9x² = : x² 2 4
= 9 : 4Correct Option: D
Using Rule 10,
Side of the given square = x cm (let)Side of new square = 3x cm. (let) 2 ∴ Required ratio of areas = 
3x 
² : x² = 9x² = : x² 2 4
= 9 : 4
- The area of a circle is 324π square cm. The length of its longest chord (in cm.) is
-
View Hint View Answer Discuss in Forum
Using Rule 14,
Area of circle = πr²
⇒ πr² = 324π
⇒ r² = 324
∴ r = √324 = 18 cm.
∴ Length of longest chord of circle = Diameter = 2 × 18 = 36 cm.Correct Option: A
Using Rule 14,
Area of circle = πr²
⇒ πr² = 324π
⇒ r² = 324
∴ r = √324 = 18 cm.
∴ Length of longest chord of circle = Diameter = 2 × 18 = 36 cm.
- The area of a rhombus is 256 square cm. and one of its diagonals is twice the other in length. Then length of its larger diagonal is
-
View Hint View Answer Discuss in Forum
Using Rule 12,
One diagonal of rhombus = d1 = x cm.
Second diagonal = d2 = 2x cm.Area of rhombus = 1 d1.d2 2 ⇒ 1 x. 2x = 256 2
⇒ x² = 256
⇒ x = 256 = 16 cm.
∴ Larger diagonal = 2x = 2 × 16 = 32 cm.Correct Option: A
Using Rule 12,
One diagonal of rhombus = d1 = x cm.
Second diagonal = d2 = 2x cm.Area of rhombus = 1 d1.d2 2 ⇒ 1 x. 2x = 256 2
⇒ x² = 256
⇒ x = 256 = 16 cm.
∴ Larger diagonal = 2x = 2 × 16 = 32 cm.
- If the side of a square is 1/2 (x + 1) units and its diagonal is (3 – x)/√2 units, then the length of the side of the square would be
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Diagonal of square = √2 × side= 3 - x = √2 × 1 (x + 1) √2 2 ⇒ 3 - x = √2 × √2 × 1 (x + 1) 2
⇒ 3 – x = x + 1
⇒ x + x = 3 –1
⇒ 2x = 2 ⇒ x = 1 unitCorrect Option: C
Using Rule 10,
Diagonal of square = √2 × side= 3 - x = √2 × 1 (x + 1) √2 2 ⇒ 3 - x = √2 × √2 × 1 (x + 1) 2
⇒ 3 – x = x + 1
⇒ x + x = 3 –1
⇒ 2x = 2 ⇒ x = 1 unit
- The circumference of a triangle is 24 cm and the circumference of its in-circle is 44 cm. Then the area of the triangle is (taking π = 22/7 )
-
View Hint View Answer Discuss in Forum
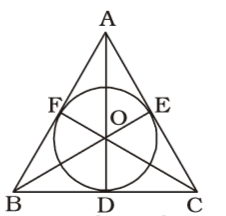
The centre of incircle is point ‘O’.
OD = OE = OF = r
∴ 2πr = 44⇒ 2 × 22 × r = 44 7 ⇒ r = 44 × 7 = 7 cm. 2 × 22
∴ Area of ∆ABC= 1 (AB + BC + CA) × r 2 = 1 × 24 × 7 = 84 square cm. 2 Correct Option: B

The centre of incircle is point ‘O’.
OD = OE = OF = r
∴ 2πr = 44⇒ 2 × 22 × r = 44 7 ⇒ r = 44 × 7 = 7 cm. 2 × 22
∴ Area of ∆ABC= 1 (AB + BC + CA) × r 2 = 1 × 24 × 7 = 84 square cm. 2

