Mensuration
- Two adjacent sides of a parallelogram are 21 cms and 20 cms. The diagonal joining the end points of these two sides is 29 cms. The area of the parallelogram (in sq. cms) is
-
View Hint View Answer Discuss in Forum
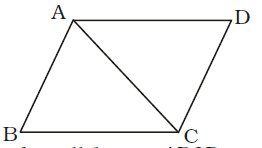
Area of parallelogram ABCD = 2 × Area of ∆ABC
AB = 21 cm. = c
BC = 20 cm. = a
AC = 29 cm. = b∴ Semi-perimeter of ∆ABC = s = a + b + c 2 = 
20 + 29 + 21 
cm. 2 = 70 = 35 cm. 2
∴ Area of ∆ABC
= √8(s – a)(s – b)(s – c)
= √35(35 – 20)(35 – 29)(35 – 21)
= √35 × 15 × 6 × 14
= √7 × 5 × 5 × 3 × 2 × 3 × 2 × 7
= 7 × 2 × 3 × 5 = 210 sq.cm.
∴ Area of ABCD = (2 × 210) sq. cm.
= 420 sq. cm.Correct Option: D

Area of parallelogram ABCD = 2 × Area of ∆ABC
AB = 21 cm. = c
BC = 20 cm. = a
AC = 29 cm. = b∴ Semi-perimeter of ∆ABC = s = a + b + c 2 = 
20 + 29 + 21 
cm. 2 = 70 = 35 cm. 2
∴ Area of ∆ABC
= √8(s – a)(s – b)(s – c)
= √35(35 – 20)(35 – 29)(35 – 21)
= √35 × 15 × 6 × 14
= √7 × 5 × 5 × 3 × 2 × 3 × 2 × 7
= 7 × 2 × 3 × 5 = 210 sq.cm.
∴ Area of ABCD = (2 × 210) sq. cm.
= 420 sq. cm.
- ∆ABC is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of ∆ABC : the area of the trapezium ADEC is
-
View Hint View Answer Discuss in Forum
Let, AB = BC = CA = 2x units
∴ BD = BE = x unitsArea of ∆ABC = √3 × (2x)² 4
= √x² sq. unitsArea of ∆BDE = √3 x² 4 ∴ Area of a trapezium ADEC = 
√3x² - √3 x² 
sq. units 4 = 3√3x² sq. unit 4 ∴ Required ratio = √3x² : 3√3 x² = 4 : 3 4 Correct Option: D
Let, AB = BC = CA = 2x units
∴ BD = BE = x unitsArea of ∆ABC = √3 × (2x)² 4
= √x² sq. unitsArea of ∆BDE = √3 x² 4 ∴ Area of a trapezium ADEC = 
√3x² - √3 x² 
sq. units 4 = 3√3x² sq. unit 4 ∴ Required ratio = √3x² : 3√3 x² = 4 : 3 4
- The perimeters of a square and a rectangle are equal . If their area be ‘A’ m&su2; and ‘B’ m&su2; respectively, then correct statement is
-
View Hint View Answer Discuss in Forum
Length of rectangle = l metre,
its breadth = b metre
Side of square = x metre
According to the question,
4x = 2 (l + b)
⇒ l + b = 2x ..... (i)
Area of square = A = x²
Area of rectangle = B = lb
∴ A – B = x² – lb= 
l + b 
² - lb 4 = l² + b² + 2lb - lb 4 = l² + b² + 2lb - 4lb 4 = (l + b)² > 0 4
⇒ A > BCorrect Option: C
Length of rectangle = l metre,
its breadth = b metre
Side of square = x metre
According to the question,
4x = 2 (l + b)
⇒ l + b = 2x ..... (i)
Area of square = A = x²
Area of rectangle = B = lb
∴ A – B = x² – lb= 
l + b 
² - lb 4 = l² + b² + 2lb - lb 4 = l² + b² + 2lb - 4lb 4 = (l + b)² > 0 4
⇒ A > B
- A rectangle with one side of length 4 cm. is inscribed in a circle of diameter 5 cm. Find, the area of the rectangle.
-
View Hint View Answer Discuss in Forum
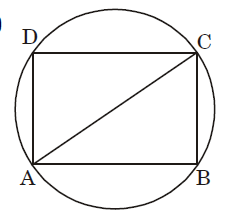
Let AB = 4 cm.
Diagonal of rectangle = Diameter of cirlce = 5 cm.
In ∆ABC,
BC = √AC² – AB²
= √5² – 4² = √25 – 16
= √9 = 3 cm.
∴ Area of rectangle = 4 × 3 = 12 sq. cm.Correct Option: B

Let AB = 4 cm.
Diagonal of rectangle = Diameter of cirlce = 5 cm.
In ∆ABC,
BC = √AC² – AB²
= √5² – 4² = √25 – 16
= √9 = 3 cm.
∴ Area of rectangle = 4 × 3 = 12 sq. cm.
- A rectangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. The area of the rectangle is :
-
View Hint View Answer Discuss in Forum
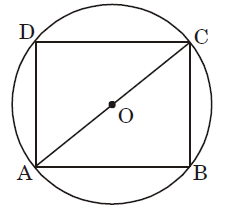
Let AB = 4 cm.
∴ AC = Diameter of circle
= Diagonal of rectangle = 5 cm.
∴ In ∆ABC
BC = √AC² – AB²
= √5² – 4² = √25 – 16
= √9 = 3 cm.
∴ Area of rectangle = 4 × 3 = 12 sq. cm.Correct Option: B

Let AB = 4 cm.
∴ AC = Diameter of circle
= Diagonal of rectangle = 5 cm.
∴ In ∆ABC
BC = √AC² – AB²
= √5² – 4² = √25 – 16
= √9 = 3 cm.
∴ Area of rectangle = 4 × 3 = 12 sq. cm.

