Mensuration
- The area of a circle is increased by 22 cm its radius is increased by 1 cm. The original radius of the circle is
-
View Hint View Answer Discuss in Forum
Using Rule 14,
Let the original radius be r cm.
According to the question,
π(r + 1)² – πr² = 22
⇒ π(r² + 2r + 1–r²) = 22⇒ (2r + l) × 22 = 22 7 ⇒ 2r + l = 22 × 7 = 7 22 ⇒ 2r = 7 - 1 = 6 ⇒ r = 6 = 3 cm. 2 Correct Option: C
Using Rule 14,
Let the original radius be r cm.
According to the question,
π(r + 1)² – πr² = 22
⇒ π(r² + 2r + 1–r²) = 22⇒ (2r + l) × 22 = 22 7 ⇒ 2r + l = 22 × 7 = 7 22 ⇒ 2r = 7 - 1 = 6 ⇒ r = 6 = 3 cm. 2
- The radius of circle A is twice that of circle B and the radius of circle B is twice that of circle C. Their area will be in the ratio
-
View Hint View Answer Discuss in Forum
Using Rule 14,
Required ratio = π(4r)² : π(2r)² : π(r)²
= 16 : 4 : 1Correct Option: A
Using Rule 14,
Required ratio = π(4r)² : π(2r)² : π(r)²
= 16 : 4 : 1
- The circumference of a circle is 11 cm and the angle of a sector of the circle is 60°. The area of
the sector is (use π = 22/7)
-
View Hint View Answer Discuss in Forum
Using Rule 17,
Let the radius of the circle be r cm.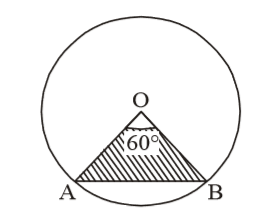
According to the question,2πr = 11 ⇒ 2 × 22 r = 11 7 ⇒ r = 11 × 7 = 7 cm. 2 × 22 4 ∴ Area of the sector AOB = θ × πr² 360° = 60° × 22 × 7 × 7 sq. cm 360° 7 4 4 = 77 = 1 29 sq.cm. 48 48 Correct Option: A
Using Rule 17,
Let the radius of the circle be r cm.
According to the question,2πr = 11 ⇒ 2 × 22 r = 11 7 ⇒ r = 11 × 7 = 7 cm. 2 × 22 4 ∴ Area of the sector AOB = θ × πr² 360° = 60° × 22 × 7 × 7 sq. cm 360° 7 4 4 = 77 = 1 29 sq.cm. 48 48
- A 7 m wide road runs outside around a circular park, whose circumference is 176 m. The area of the road is :
[use π = 22/7 ]
-
View Hint View Answer Discuss in Forum
Using Rule 14,
If the radius of the circular park be r metre, then 2πr = 176= 2 × 22 × r = 176 7 ⇒ r = 176 × 7 = 28 metre 2 × 22
Radius of the park with road = 28 + 7 = 35 metre∴ Area of the road = 22 (35² - 28²) 7 = 22 × 63 × 7 = 1386 m² 7 Correct Option: A
Using Rule 14,
If the radius of the circular park be r metre, then 2πr = 176= 2 × 22 × r = 176 7 ⇒ r = 176 × 7 = 28 metre 2 × 22
Radius of the park with road = 28 + 7 = 35 metre∴ Area of the road = 22 (35² - 28²) 7 = 22 × 63 × 7 = 1386 m² 7
- The four equal circles of radius 4 cm drawn on the four corners of a square touch each other externally. Then the area of the portion between the square and the four sectors is
-
View Hint View Answer Discuss in Forum
Using Rule 10 and 14,

Side of the square = 8 cm
∴ Area of the square = 8 × 8 = 64 sq.cm.
Area of the four sectors = π × 4² = 16π sq.cm.
∴ Required area = 64 – 16π
= 16 (4 – π) sq.cm.Correct Option: D
Using Rule 10 and 14,

Side of the square = 8 cm
∴ Area of the square = 8 × 8 = 64 sq.cm.
Area of the four sectors = π × 4² = 16π sq.cm.
∴ Required area = 64 – 16π
= 16 (4 – π) sq.cm.

