Mensuration
- In an equilateral triangle of side 24 cm, a circle is inscribed touching its sides. The area of the remaining portion of the triangle is (√3 = 1732)
-
View Hint View Answer Discuss in Forum
Using Rule 18, 6 and 14,
In-radius = a 2√3 = 24 = 4√3 cm 2√3 Arae of triangle = √3 × (side)² 4 = √3 × 24 × 24 4
= 144√3 sq.cm.
= 144 × 1.732 = 249.408 sq.cm.
Area of circle = πr²= 22 × 4√3 × 4√3 7 = 1056 = 150.86 sq.cm. 7
Area of remaining part = (249.408 – 150.86) sq.cm.
= 98.548 sq.cm.
≈ 98.55 sq.cm.Correct Option: A
Using Rule 18, 6 and 14,
In-radius = a 2√3 = 24 = 4√3 cm 2√3 Arae of triangle = √3 × (side)² 4 = √3 × 24 × 24 4
= 144√3 sq.cm.
= 144 × 1.732 = 249.408 sq.cm.
Area of circle = πr²= 22 × 4√3 × 4√3 7 = 1056 = 150.86 sq.cm. 7
Area of remaining part = (249.408 – 150.86) sq.cm.
= 98.548 sq.cm.
≈ 98.55 sq.cm.
- Two sides of a plot measuring 32 m and 24 m and the angle between them is a perfect right angle. The other two sides measure 25 m each and the other three angles are not right angles. The area of the plot in m² is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
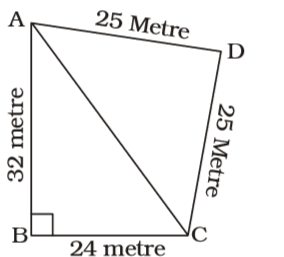
AC = √AB² + BC²
= √32² + 24²
= √1024 + 576 = √1600
= 40 metre∴ Area of ∆ABC = 1 × BC × AB 2 = 1 × 24 × 32 2
= 384 sq. metre
Semi-peri meter of ∆ADC (s)= 25 + 25 + 40 2 = 90 = 45 metre 2
∴ Area of ∆ADC = √s(s - a)(s - b)(s - c)
= √45(45 - 25)(45 - 25)(45 - 40)
= √45 × 20 × 20 × 5
= 20 × 15 = 300 sq. metre
∴ Area of the plot = 384 + 300 = 684 sq.metreCorrect Option: D
Using Rule 1,

AC = √AB² + BC²
= √32² + 24²
= √1024 + 576 = √1600
= 40 metre∴ Area of ∆ABC = 1 × BC × AB 2 = 1 × 24 × 32 2
= 384 sq. metre
Semi-peri meter of ∆ADC (s)= 25 + 25 + 40 2 = 90 = 45 metre 2
∴ Area of ∆ADC = √s(s - a)(s - b)(s - c)
= √45(45 - 25)(45 - 25)(45 - 40)
= √45 × 20 × 20 × 5
= 20 × 15 = 300 sq. metre
∴ Area of the plot = 384 + 300 = 684 sq.metre
- a and b are two sides adjacent to the right angle of a right-angled triangle and p is the perpendicular drawn to the hypotenuse from the opposite vertex. Then p2 is equal to
-
View Hint View Answer Discuss in Forum
Using Rule 1,
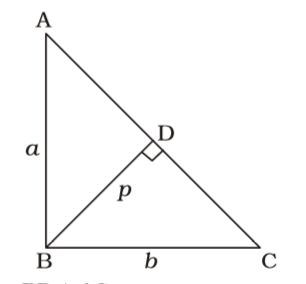
BD ⊥ AC
AB ⊥ BC
Hypotenuse of ∆ABC = √AB² + BC²
= √a² + b²Area of ∆ABC = 1 × AB × BC 2 = 1 × AC × BD 2
⇒AB × BC = AC × BD
⇒ ab = √a² + b² × p
On squaring both sides,
a²b² = (a² + b²) p²∴ p² = a²b² a² + b² Correct Option: C
Using Rule 1,

BD ⊥ AC
AB ⊥ BC
Hypotenuse of ∆ABC = √AB² + BC²
= √a² + b²Area of ∆ABC = 1 × AB × BC 2 = 1 × AC × BD 2
⇒AB × BC = AC × BD
⇒ ab = √a² + b² × p
On squaring both sides,
a²b² = (a² + b²) p²∴ p² = a²b² a² + b²
- A is the centre of circle whose radius is 8 and B is the centre of a circle whose diameter is 8. If these two circles touch externally, then the area of the circle with diameter AB is
-
View Hint View Answer Discuss in Forum
Using Rule 14,
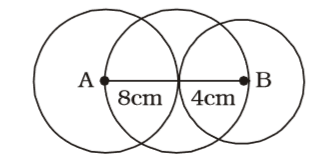
Diameter = AB = 8 + 4 = 12 unitsRadius = 12 = 6 units 2
∴ Area of circle = πr² = π × 6²
= 36π sq. unitsCorrect Option: A
Using Rule 14,

Diameter = AB = 8 + 4 = 12 unitsRadius = 12 = 6 units 2
∴ Area of circle = πr² = π × 6²
= 36π sq. units
- The length of a rectangle is increased by 10% and breadth decreased by 10%. The area of the new rectangle is
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Change in area = -10 × 10 = - 1 % 100
% Negative sign shows decrease.Correct Option: D
Using Rule 10,
Change in area = -10 × 10 = - 1 % 100
% Negative sign shows decrease.

