Mensuration
- A hemispherical cup of radius 4 cm is filled to the brim with coffee. The coffee is then poured into a vertical cone of radius 8 cm and height 16 cm. The percentage of the volume of the cone that remains empty is :
-
View Hint View Answer Discuss in Forum
Volume of the hemispherical cup = 2 πr³ 3 Volume of the hemispherical cup = 2 π × 4 × 4 × 4 3 = 128π cu.cm. 3 Volume of cone = 1 πr²h 3 = 1 π × 8 × 8 × 16 3 = 128 × 8π cu.cm. 3
Part filled = 1/8
∴ Part remaining empty = 7/8
= 87.5%Correct Option: A
Volume of the hemispherical cup = 2 πr³ 3 Volume of the hemispherical cup = 2 π × 4 × 4 × 4 3 = 128π cu.cm. 3 Volume of cone = 1 πr²h 3 = 1 π × 8 × 8 × 16 3 = 128 × 8π cu.cm. 3
Part filled = 1/8
∴ Part remaining empty = 7/8
= 87.5%
- The volume (in m3) of rain water that can be collected from 1.5 hectares of ground in a rainfall of 5 cm is
-
View Hint View Answer Discuss in Forum
1 hectare = 10000 sq.metre then Area of the ground = 15000 sq.metre
∴ Required volume = 15000 × 5 = 750 cubic m. 100 Correct Option: B
1 hectare = 10000 sq.metre then Area of the ground = 15000 sq.metre
∴ Required volume = 15000 × 5 = 750 cubic m. 100
- Each edge of a regular tetrahedron is 3 cm, then its volume is
-
View Hint View Answer Discuss in Forum
Area of the tetrahedron = 1 area of base × height 3 Area of the base = √3 × (side)² 4 = √3 × 3 × 3 = 9√3 cm² 4 4
Now, length of the perpendicular in the equilateral triangle= √3² - 
3 
² 2 = √9 - 9 = 3√3 cm 4 2 ∴ Height = √ 
3√3 
² - 
√3 
² 2 2 = √ 27 - 3 = √6 cm. 4 4 ∴ Required area = 1 × 9√3 × √6 = 9√3 cu.cm. 3 4 4 Correct Option: A
Area of the tetrahedron = 1 area of base × height 3 Area of the base = √3 × (side)² 4 = √3 × 3 × 3 = 9√3 cm² 4 4
Now, length of the perpendicular in the equilateral triangle= √3² - 
3 
² 2 = √9 - 9 = 3√3 cm 4 2 ∴ Height = √ 
3√3 
² - 
√3 
² 2 2 = √ 27 - 3 = √6 cm. 4 4 ∴ Required area = 1 × 9√3 × √6 = 9√3 cu.cm. 3 4 4
- The perimeter of the triangular base of a right prism is 15 cm and radius of the incircle of the triangular base is 3 cm. If the volume of the prism be 270 cm³, then the height of the prism is
-
View Hint View Answer Discuss in Forum
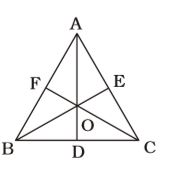
Radius of the in-circle = OE = OD = OF = 3 cmArea of triangular base = 
1 AB × OF + 1 × BC × OD + 1 × AC × OE 
2 2 2 = 1 × 3(AB + BC + AC) = 1 × 3 × 15 = 45 sq.cm. 2 2 2
Volume of the prism = Area of the base × height⇒ 270 = 45 × height 2 ∴ height = 270 × 2 = 12 cm. 45 Correct Option: D

Radius of the in-circle = OE = OD = OF = 3 cmArea of triangular base = 
1 AB × OF + 1 × BC × OD + 1 × AC × OE 
2 2 2 = 1 × 3(AB + BC + AC) = 1 × 3 × 15 = 45 sq.cm. 2 2 2
Volume of the prism = Area of the base × height⇒ 270 = 45 × height 2 ∴ height = 270 × 2 = 12 cm. 45
- A prism has as the base a right angled triangle whose sides adjacent to the right angles are 10 cm and 12 cm long. The height of the prism is 20 cm. The density of the material of the prism is 6 gm/cubic cm. The weight of the prism is
-
View Hint View Answer Discuss in Forum
Area of the base of prism = 1 × 10 × 12 = 60 sq. cm. 2
∴ Volume of prism = Area of the base × height = 60 × 20 =1200 cu.cm
∴ Mass of prism = Volume × density = (1200 × 6) gm= 
1200 × 6 
kg. = 7.2 kg. 1000 Correct Option: B
Area of the base of prism = 1 × 10 × 12 = 60 sq. cm. 2
∴ Volume of prism = Area of the base × height = 60 × 20 =1200 cu.cm
∴ Mass of prism = Volume × density = (1200 × 6) gm= 
1200 × 6 
kg. = 7.2 kg. 1000

