Mensuration
- ∆ABC is similar to ∆DEF. The ratio of their perimeters is 4 : 1. The ratio of their areas is
-
View Hint View Answer Discuss in Forum
∆ABC ~ ∆DEF∴ AB = BC = AC DE EF DF = AB + BC + AC = 4 DE + EF + DF 1 ∴ Area of ∆ABC = AB² = 16 = 16 : 1 Area of ∆DEF DE² 1 Correct Option: B


∆ABC ~ ∆DEF∴ AB = BC = AC DE EF DF = AB + BC + AC = 4 DE + EF + DF 1 ∴ Area of ∆ABC = AB² = 16 = 16 : 1 Area of ∆DEF DE² 1
- In ∆ABC, a line through A cuts the side BC at D such that BD : DC = 4 : 5. If the area of ∆ABD = 60 cm², then the area of ∆ADC is
-
View Hint View Answer Discuss in Forum
Using Rule 1, A
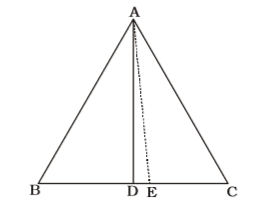
Let, AE ⊥ BC∴ Area of ∆ABD Area of ∆ADC = √1 × BD × AE 2 1 × CD × AE 2 ⇒ 60 = BD ∆ADC CD = 60 = 4 ∆ADC 5 ∆ADC = A60 × 5 4
= 75 sq. cm.Correct Option: D
Using Rule 1, A

Let, AE ⊥ BC∴ Area of ∆ABD Area of ∆ADC = √1 × BD × AE 2 1 × CD × AE 2 ⇒ 60 = BD ∆ADC CD = 60 = 4 ∆ADC 5 ∆ADC = A60 × 5 4
= 75 sq. cm.
- In a rhombus ABCD, ∠A = 60° and AB = 12 cm. Then the diagonal BD is
-
View Hint View Answer Discuss in Forum
In the rhombus ABCD, AB = AD = 12 cm.
∠BAD = 60°
∴ ∠ABD = ∠ADB = 60°
∴ BD = 12 cm. because ∆ABD is an equilateral triangle.Correct Option: D
In the rhombus ABCD, AB = AD = 12 cm.
∠BAD = 60°
∴ ∠ABD = ∠ADB = 60°
∴ BD = 12 cm. because ∆ABD is an equilateral triangle.
- If two medians BE and CF of a triangle ABC, intersect each other at G and if BG = CG, ∠BGC = 60° and BC = 8 cm then area of the triangle ABC is
-
View Hint View Answer Discuss in Forum
Using Rule 6,
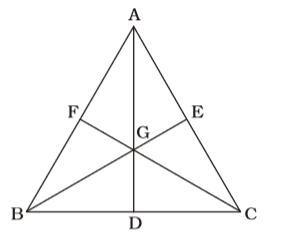
∠BGC = 60° BG = GC
∴ ∠GBC = ∠GCB = 60°
∴ ∆GBC is an equilateral triangle.
∴ Area of ∆GBC= √3 × 8² 4
= 16√3 sq. cm.
∴ Area of ∆ABC = 3 × 16√3 = 48√3 sq. cm.Correct Option: C
Using Rule 6,

∠BGC = 60° BG = GC
∴ ∠GBC = ∠GCB = 60°
∴ ∆GBC is an equilateral triangle.
∴ Area of ∆GBC= √3 × 8² 4
= 16√3 sq. cm.
∴ Area of ∆ABC = 3 × 16√3 = 48√3 sq. cm.
- Two circles touch each other externally. The sum of their areas is 130π sq cm and the distance between their centres is 14 cm. The radius of the smaller circle is
-
View Hint View Answer Discuss in Forum
Using Rule 14,

OO' = r1 + r2 = 14 cm. --(i)
Again, πr1² + πr2² = 130π
⇒ r1² + r2² = 130
⇒ r1² + (14 – r1)² = 130
[From equation (i)]
⇒ r1² + 196 – 28r1 + r1²= 130
⇒ 2r1² – 28r1 + 196 – 130 = 0
⇒ 2r1² – 28r1 + 66 = 0
⇒ r1² – 14r1 + 33 = 0
⇒ r1² – 11r1 – 3r1 + 33 = 0
⇒ r1 (r1 –11) – 3 (r1 –11) = 0
⇒ (r1 –11) (r1 – 3) = 0
⇒ r1 = 11 or] 3 cm.
∴ r2 = 3 or] 11 cm.Correct Option: D
Using Rule 14,

OO' = r1 + r2 = 14 cm. --(i)
Again, πr1² + πr2² = 130π
⇒ r1² + r2² = 130
⇒ r1² + (14 – r1)² = 130
[From equation (i)]
⇒ r1² + 196 – 28r1 + r1²= 130
⇒ 2r1² – 28r1 + 196 – 130 = 0
⇒ 2r1² – 28r1 + 66 = 0
⇒ r1² – 14r1 + 33 = 0
⇒ r1² – 11r1 – 3r1 + 33 = 0
⇒ r1 (r1 –11) – 3 (r1 –11) = 0
⇒ (r1 –11) (r1 – 3) = 0
⇒ r1 = 11 or] 3 cm.
∴ r2 = 3 or] 11 cm.
-