Mensuration
- The length of a median of an equilateral triangle is 12 3 cms. Then the area of the triangle is :
-
View Hint View Answer Discuss in Forum
Median of equilateral triangle = Its height = 12√3 cm.
If the side of equilateral triangle be x cm, then its height= √3 x cm 2 = √3 x cm = 12√3 2 ⇒ x = 12√3 × 2 = 24 cm √3 ∴ Required area = 
√3 × 24 × 24 
sq. cm 4
= 144√3 sq. cm.Correct Option: C
Median of equilateral triangle = Its height = 12√3 cm.
If the side of equilateral triangle be x cm, then its height= √3 x cm 2 = √3 x cm = 12√3 2 ⇒ x = 12√3 × 2 = 24 cm √3 ∴ Required area = 
√3 × 24 × 24 
sq. cm 4
= 144√3 sq. cm.
- Three equal circles of unit radius touch one another. Then the area of the circle circumscribing the three circles is
-
View Hint View Answer Discuss in Forum
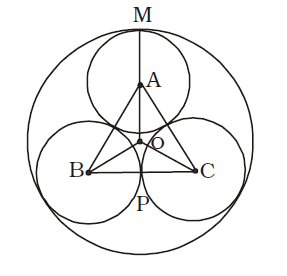
AB = BC = AC = 2 cm.
(∵ Radius of each circle = 1 cm.)∴ AP = √3 × 2 = √3 cm. 2
Point O is the centroid.OA = 2 × √3 = 2 3 √3 OM = 2 + 1 = 2 + √3 cm. √3 √3
OM = radius of larger circle
∴ Required area = πR²= 
2 + √3 
² √3 = π (2 + √3)² 3 Correct Option: C

AB = BC = AC = 2 cm.
(∵ Radius of each circle = 1 cm.)∴ AP = √3 × 2 = √3 cm. 2
Point O is the centroid.OA = 2 × √3 = 2 3 √3 OM = 2 + 1 = 2 + √3 cm. √3 √3
OM = radius of larger circle
∴ Required area = πR²= 
2 + √3 
² √3 = π (2 + √3)² 3
- Area of the circle inscribed in a square of diagonal 6√2 cm. (in sq. cm.) is
-
View Hint View Answer Discuss in Forum

Diagonal of square = 6√2 cm.∴ Side of square = 6√2 = 6 cm. √2
∴ Diameter of circle = 6 cm.
Its radius = 3 cm.
∴ Area of circle = πr⊃
= π(3)² sq. cm.
= 9π sq. cm.Correct Option: A

Diagonal of square = 6√2 cm.∴ Side of square = 6√2 = 6 cm. √2
∴ Diameter of circle = 6 cm.
Its radius = 3 cm.
∴ Area of circle = πr⊃
= π(3)² sq. cm.
= 9π sq. cm.
- The diagonals of two squares are in the ratio 5 : 2. The ratio of their area is
-
View Hint View Answer Discuss in Forum
Area of square = 1 × (diagonal)² 2 ∴ Required ratio = 1 (d1)² 2 1 (d2)² 2 = 
d1 
² = 
5 
² = 25 d2 2 4 Correct Option: B
Area of square = 1 × (diagonal)² 2 ∴ Required ratio = 1 (d1)² 2 1 (d2)² 2 = 
d1 
² = 
5 
² = 25 d2 2 4
- In ∆ABC and ∆PQR, ∠B = ∠Q, ∠C = ∠R. M is the midpoint of side QR. If AB : PQ = 7 : 4, then
area(∆ABC) is : area(∆PMR) 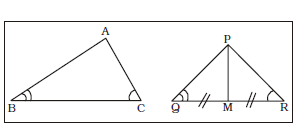
-
View Hint View Answer Discuss in Forum

M is the mid point of QR.
∴ PM is the median.
∴ ∆PMQ and ∆PMR are equal in area.
∠B = Q, ∠C = ∠R
By AA - similarity theorem,
∆ABC ~ ∆PQR∴ ∆ABC = AB² = 
7 
² ∆PQR PQ² 4 ⇒ ∆ABC = 49 2∆PMR 16 ⇒ ∆ABC = 49 × 2 = 49 2∆PMR 16 8 Correct Option: C


M is the mid point of QR.
∴ PM is the median.
∴ ∆PMQ and ∆PMR are equal in area.
∠B = Q, ∠C = ∠R
By AA - similarity theorem,
∆ABC ~ ∆PQR∴ ∆ABC = AB² = 
7 
² ∆PQR PQ² 4 ⇒ ∆ABC = 49 2∆PMR 16 ⇒ ∆ABC = 49 × 2 = 49 2∆PMR 16 8

