Mensuration

Mensuration

Easy Questions
Moderate Questions
Difficult Questions

Aptitude

Simplification
Number System
Fractions
Elementary Algebra
LCM and HCF
Approximation
Unitary Method
Linear Equation
Quadratic Equation
Discount
Average
Surds and Indices
Percentage
Square root and cube root
Order of Magnitude
Work and Wages
Odd Man Out and Series
Algebra
Profit and Loss
Stocks and Shares
True Discount
Ratio, Proportion
Partnership
Alligation or Mixture
Time and Work
Pipes and Cistern
Speed, Time and Distance
Problem on Trains
Height and Distance
Banker's Discount
Boats and Streams
Races and games
Problems on Ages
Clocks and Calendars
Simple interest
Compound Interest
Sets and Functions
Area and Perimeter
Volume and Surface Area of Solid Figures
Sequences and Series
Plane Geometry
Logarithm
Probability
Permutation and Combination
Statistics
Mensuration
Trigonometry
Aptitude miscellaneous
  1. If each edge of a cube is increased by 50%, the percentage increase in its surface area is








  1. View Hint View Answer Discuss in Forum

    Percentage increase = 50 + 50 +
    50 × 50
    		 % = 125 %
    100

    Correct Option: D

    Percentage increase = 50 + 50 +
    50 × 50
    		 % = 125 %
    100

  1. Three solid iron cubes of edges 4 cm, 5 cm and 6 cm are melted together to make a new cube. 62 cm² of the melted material is lost due to improper handling. The area (in cm²) of the whole surface of the newly formed cube is








  1. View Hint View Answer Discuss in Forum

    Volume of all three cubes = (4² + 5² + 6²) cu.cm.
    = (64 + 125 + 216) cu.cm. = 405 cu.cm.
    ∴ Volume of new cube = 405 – 62 = 343 cu.cm.
    ∴ Edge of cube = ³√343 = 7 cm.
    ∴ Surface area = 6 × 7² = 294 sq. cm.

    Correct Option: A

    Volume of all three cubes = (4² + 5² + 6²) cu.cm.
    = (64 + 125 + 216) cu.cm. = 405 cu.cm.
    ∴ Volume of new cube = 405 – 62 = 343 cu.cm.
    ∴ Edge of cube = ³√343 = 7 cm.
    ∴ Surface area = 6 × 7² = 294 sq. cm.

  1. A square of side 3 cm is cut off from each corner of a rectangular sheet of length 24 cm and breadth 18 cm and the remaining sheet is folded to form an open rectangular box. The surface area of the box is








  1. View Hint View Answer Discuss in Forum


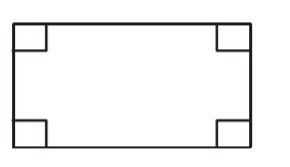
    Length of box = 24 –( 2 × 3) = 18 cm
    Width of box = 18 – 2 × 3 = 12 cm
    Height of box = 3 cm
    ∴ Surface area of box = 18 × 12 + 2 (12 × 3 + 3 × 18)
    = 216 + 180 = 396 sq. cm

    Correct Option: B


    Length of box = 24 –( 2 × 3) = 18 cm
    Width of box = 18 – 2 × 3 = 12 cm
    Height of box = 3 cm
    ∴ Surface area of box = 18 × 12 + 2 (12 × 3 + 3 × 18)
    = 216 + 180 = 396 sq. cm

  1. A solid right circular cylinder and a solid hemisphere stand on equal bases and have the same height. The ratio of their whole surface area is:








  1. View Hint View Answer Discuss in Forum

    Radius of cylinder = r units and height = r units
    [∵ height of hemisphere = radius]
    ∴ Required ratio = 2πr² + 2πr² : 2πr² + πr²
    = 4 : 3

    Correct Option: C

    Radius of cylinder = r units and height = r units
    [∵ height of hemisphere = radius]
    ∴ Required ratio = 2πr² + 2πr² : 2πr² + πr²
    = 4 : 3

  1. The base of a cone and a cylinder have the same radius 6 cm. They have also the same height 8 cm. The ratio of the curved surface of the cylinder to that of the cone is








  1. View Hint View Answer Discuss in Forum

    Slant height of cone l = √6² + 8²
    = √36 + 64 = √100 = 10 cm
    ∴ Curved surface of cylinder : Curved surface of cone = 2πrh : πrl
    = 2h : l = 16 : 10 = 8 : 5

    Correct Option: A

    Slant height of cone l = √6² + 8²
    = √36 + 64 = √100 = 10 cm
    ∴ Curved surface of cylinder : Curved surface of cone = 2πrh : πrl
    = 2h : l = 16 : 10 = 8 : 5