Mensuration
- The areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
-
View Hint View Answer Discuss in Forum
Using Rule 14,
Area of circle = πr²
Area of square = x²
According to the question, x² = πr² π x = √πr∴ Required ratio = x = √πr = √π : 1 r r Correct Option: C
Using Rule 14,
Area of circle = πr²
Area of square = x²
According to the question, x² = πr² π x = √πr∴ Required ratio = x = √πr = √π : 1 r r
- ABCD is a square inscribed in a circle of radius r. Then the total area (in square units) of the portions of the circle lying outside the square is
-
View Hint View Answer Discuss in Forum
Using Rule 10 and 14,
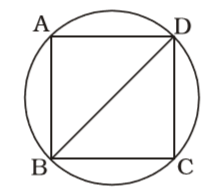
Radius of circle = r units
Area of circle = πr² sq. units
In square ABCD Diagonal = BD = 2r units∴ Area of square = 1 × (2r)² = 2r² 2
∴ Required difference = πr² – 2r² = r² (π – 2) sq. unitsCorrect Option: D
Using Rule 10 and 14,

Radius of circle = r units
Area of circle = πr² sq. units
In square ABCD Diagonal = BD = 2r units∴ Area of square = 1 × (2r)² = 2r² 2
∴ Required difference = πr² – 2r² = r² (π – 2) sq. units
- The lengths of the two parallel sides of a trapezium are 28 cm and 40 cm. If the length of each of its other two sides be 12 cm, then the area (in cm2) of the trapezium is
-
View Hint View Answer Discuss in Forum
Using Rule 9 and 1,

AE = FB = 6 cm.
In ∆ADE,
DE = √AD² - AE²
= √12² - 6²
= √(12 + 6)(12 - 6)
= √18 × 6
= 6√3cm
∴ Area of CDEF = 28 × 6√3 = 168√3 sq. cm.
Area of ∆ADE= 1 × AE × DE 2 = 1 × 6 × 6√3 2
= 18√3 sq. cm.
∴ Area of trapezium = (168√3 + 2 × 18√3)sq. cm.
= 204√3 sq. cm.Correct Option: C
Using Rule 9 and 1,

AE = FB = 6 cm.
In ∆ADE,
DE = √AD² - AE²
= √12² - 6²
= √(12 + 6)(12 - 6)
= √18 × 6
= 6√3cm
∴ Area of CDEF = 28 × 6√3 = 168√3 sq. cm.
Area of ∆ADE= 1 × AE × DE 2 = 1 × 6 × 6√3 2
= 18√3 sq. cm.
∴ Area of trapezium = (168√3 + 2 × 18√3)sq. cm.
= 204√3 sq. cm.
- The perimeter of a sheet of paper in the shape of a quadrant of a circle is 75 cm. Its area would be (π = 22/7)
-
View Hint View Answer Discuss in Forum

If the radius of circle be r cm, then
Perimeter of quadrant OAB = OA + AB + OB= r + 2πr + r πr + 2r 4 2 ∴ πr + 2r = 75 2 ⇒ r 
π + 2 
= 75 2 ⇒ r 
22 + 2 
= 75 7 × 2 ⇒ r × 50 = 75 14 ⇒ r = 75 × 14 = 21 cm 50 ∴ Required area = πr² 4 = 
22 × 21 × 21 
sq. cm. 7 × 4
= 346.5 sq.cm.Correct Option: B

If the radius of circle be r cm, then
Perimeter of quadrant OAB = OA + AB + OB= r + 2πr + r πr + 2r 4 2 ∴ πr + 2r = 75 2 ⇒ r 
π + 2 
= 75 2 ⇒ r 
22 + 2 
= 75 7 × 2 ⇒ r × 50 = 75 14 ⇒ r = 75 × 14 = 21 cm 50 ∴ Required area = πr² 4 = 
22 × 21 × 21 
sq. cm. 7 × 4
= 346.5 sq.cm.
- The diagonal of a quadrilateral shaped field is 24m and the perpendiculars dropped on it from the remaining opposite vertices are 8m and 13m. The area of the field is
-
View Hint View Answer Discuss in Forum
Using Rule 1,

AC = 24 metre
BE = 8 metre
DF = 13 metre
∴ Area of quadrilateral ABCD
= Area of ∆ABC + Area of ∆ACD= 1 × AC × BE + 1 × AC × DF 2 2 = 1 (24 × 8 + 24 × 13 2 = 1 × 24 (18 + 13) 2 = 1 × 24 × 21 = 252 sq metre 2 Correct Option: A
Using Rule 1,

AC = 24 metre
BE = 8 metre
DF = 13 metre
∴ Area of quadrilateral ABCD
= Area of ∆ABC + Area of ∆ACD= 1 × AC × BE + 1 × AC × DF 2 2 = 1 (24 × 8 + 24 × 13 2 = 1 × 24 (18 + 13) 2 = 1 × 24 × 21 = 252 sq metre 2
-
-
-