Mensuration
- A can go round a circular path 8 times in 40 minutes. If the diameter of the circle is increased to 10 times the original diameter, the time required by A to go round the new path once travelling at the same speed as before is :
-
View Hint View Answer Discuss in Forum
Using Rule 7,
Circumference = 2πr = 44 × r metre 7
Distance covered in 8 times = 16πr metres∴ Speed = Distance Time = 16πr m/minute 40 = 2πr m/minute 5
New circumference = 2πr × 10 = 20 πr∴ Required time = 20πr × 5 minute = 50 minute 2πr Correct Option: C
Using Rule 7,

Circumference = 2πr = 44 × r metre 7
Distance covered in 8 times = 16πr metres∴ Speed = Distance Time = 16πr m/minute 40 = 2πr m/minute 5
New circumference = 2πr × 10 = 20 πr∴ Required time = 20πr × 5 minute = 50 minute 2πr
- Find the diameter of a wheel that makes 113 revolutions to go 2 km 26 decameters. (Take p = 22 7 )
-
View Hint View Answer Discuss in Forum
Using Rule 7,
The distance covered = 2 km 26 decameters
= (2 ×1000 + 26 × 10) m. = 2260 m.The distance covered in one revolution = Total distance Number of revolutions = 2260 = 20 m. 113
Clearly,
Circumference of wheel = distance covered in 1 revolution = 20 m π × diameter = 20 m.Diameter = 20 = 20 × 7 π 22 = 70 = 6 4 m 11 11 Correct Option: B
Using Rule 7,
The distance covered = 2 km 26 decameters
= (2 ×1000 + 26 × 10) m. = 2260 m.The distance covered in one revolution = Total distance Number of revolutions = 2260 = 20 m. 113
Clearly,
Circumference of wheel = distance covered in 1 revolution = 20 m π × diameter = 20 m.Diameter = 20 = 20 × 7 π 22 = 70 = 6 4 m 11 11
- The radius of a circular wheel is 1.75 m. The number of revolutions that it will make in travelling 11 km., is
-
View Hint View Answer Discuss in Forum
Using Rule 7,
Distance covered in 1 revolution = Circumference of wheel= 2 × 22 × 1.75 m. 7 ∴ Number of revolutions = 11 × 1000 2 × 22 × 1.75 7 = 11 × 7 × 1000 = 1000 2 × 22 × 1.75 Correct Option: A
Using Rule 7,
Distance covered in 1 revolution = Circumference of wheel= 2 × 22 × 1.75 m. 7 ∴ Number of revolutions = 11 × 1000 2 × 22 × 1.75 7 = 11 × 7 × 1000 = 1000 2 × 22 × 1.75
- The area of a rhombus having one side 10 cm and one diagonal 12 cm is
-
View Hint View Answer Discuss in Forum
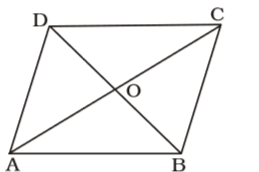
The diagonals of a rhombus bisect each other at right angles.
Let, AB = 10 cm.
AC = 12 cm.
∴ OA = OC = 6 cm.
∠AOB = 90°
∴ OB = √AB² - OA²
= √10² - 6² = √100 - 36
= √64 = 8 cm.
∴ BD = 2 × OB = 16 cm.∴ Area of rhombus = 1 d1d2 2 = 1 × 12 × 16 = 96 sq. cm. 2 Correct Option: B

The diagonals of a rhombus bisect each other at right angles.
Let, AB = 10 cm.
AC = 12 cm.
∴ OA = OC = 6 cm.
∠AOB = 90°
∴ OB = √AB² - OA²
= √10² - 6² = √100 - 36
= √64 = 8 cm.
∴ BD = 2 × OB = 16 cm.∴ Area of rhombus = 1 d1d2 2 = 1 × 12 × 16 = 96 sq. cm. 2
- Two circles touch externally. The sum of their areas is 130p sq. cm. and the distance between their centres is 14 cm. The radius of the bigger circle is (Take π = 22/7)
-
View Hint View Answer Discuss in Forum
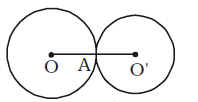
Let OA = R and O’A = r cm.
According to the question,
πR² + πr² = 130π
⇒ R² + r² = 130 ..... (i)
Again, R + r = 14 cm.
⇒ r = (14 – R) cm.
∴ R² + r² = 130
⇒ R² + (14 – R)² = 130
⇒ R² + 196 – 28R + R² = 130
⇒ 2R² – 28R + 196 – 130 = 0
⇒ 2R² – 28R + 66 = 0
⇒ R² – 14R + 33 = 0
⇒ R² – 11R – 3R + 33 = 0
⇒ R (R – 11) – 3 (R – 11) = 0
⇒ (R – 11) (R – 3) = 0
⇒ R = 11 or 3 cm.
∴ r = 3 or 11 cm.
∴ Radius of larger circle
= 11 cm.Correct Option: B

Let OA = R and O’A = r cm.
According to the question,
πR² + πr² = 130π
⇒ R² + r² = 130 ..... (i)
Again, R + r = 14 cm.
⇒ r = (14 – R) cm.
∴ R² + r² = 130
⇒ R² + (14 – R)² = 130
⇒ R² + 196 – 28R + R² = 130
⇒ 2R² – 28R + 196 – 130 = 0
⇒ 2R² – 28R + 66 = 0
⇒ R² – 14R + 33 = 0
⇒ R² – 11R – 3R + 33 = 0
⇒ R (R – 11) – 3 (R – 11) = 0
⇒ (R – 11) (R – 3) = 0
⇒ R = 11 or 3 cm.
∴ r = 3 or 11 cm.
∴ Radius of larger circle
= 11 cm.

