481. Three medians AD, BE and CF of DABC intersect at G. The area of ∆ABC is 36 sq. cm. Then the area of ∆CGE is
     

1. 1. 12 sq. cm.
      

   
   
   

   2. 6 sq. cm.
      

   
   
   

   3. 9 sq. cm.
      

   
   
   

   4. 18 sq. cm.

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
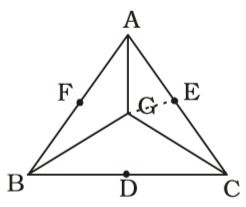
   Medians intersect at point G.
   ∴ ∆ABG = ∆BGC = ∆AGC.
   GE bisects ∆CGE.
   ∴ ∆AGE = ∆CGE
   ∴ Area of ∆CGE
   

   =	1	× Area of ∆ABC
   	6

   
   

   =	1	× 36 = 6 sq.cm.
   	6

   Correct Option: B

   
   Medians intersect at point G.
   ∴ ∆ABG = ∆BGC = ∆AGC.
   GE bisects ∆CGE.
   ∴ ∆AGE = ∆CGE
   ∴ Area of ∆CGE
   

   =	1	× Area of ∆ABC
   	6

   
   

   =	1	× 36 = 6 sq.cm.
   	6

---

482. The length of the two parallel sides of a trapezium are 16m and 20m respectively. If its height is 10m, its area in square metre is
     

1. 1. 360
      

   
   
   

   2. 260
      

   
   
   

   3. 240
      

   
   
   

   4. 180

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Area of trapezium =	1	(sum of parallel sides) × perpendicular distance
   	2

   
   

   =	1	(20 + 16) × 10
   	2

   
   

   =	1	× 36 × 10 = 180 sq. metre
   	2

   Correct Option: D

   Area of trapezium =	1	(sum of parallel sides) × perpendicular distance
   	2

   
   

   =	1	(20 + 16) × 10
   	2

   
   

   =	1	× 36 × 10 = 180 sq. metre
   	2

---

---

483. If h, C, V are respectively the height, the curved surface and the volume of a cone, then 3πVh³ – C²h² + 9V² = ?

1. 1. 0
      

   
   
   

   2. 3
      

   
   
   

   3. 1/2
      

   
   
   

   4. 11

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Slant height = l units Radius = r units
   

   ∴ l = √r² + h² , V =	1	πr²h , C = πrl
   	3

   
   ∴ 3πVh³ - C²h² + 9V²
   

   = 3π ×	1	πr²h × - (πrl)²h² +		1	πr²h
   	3			3

   
   = π²r²h⁴ - π²r²l²h² + π²r⁴h²
   = π²r²h⁴ - π²r²h²(r² + h²) + π²r⁴h²
   = π²r²h⁴ - π²r⁴h² - π²r⁴h²
   = 0

   Correct Option: A

   Slant height = l units Radius = r units
   

   ∴ l = √r² + h² , V =	1	πr²h , C = πrl
   	3

   
   ∴ 3πVh³ - C²h² + 9V²
   

   = 3π ×	1	πr²h × - (πrl)²h² +		1	πr²h
   	3			3

   
   = π²r²h⁴ - π²r²l²h² + π²r⁴h²
   = π²r²h⁴ - π²r²h²(r² + h²) + π²r⁴h²
   = π²r²h⁴ - π²r⁴h² - π²r⁴h²
   = 0

---

484. A right circular cylindrical tunnel of diameter 5m and length 10m is to be constructed from a sheet of iron. The area of iron sheet required will be :
     

1. 1. 52π
      

   
   
   

   2. 50π
      

   
   
   

   3. 51π
      

   
   
   

   4. 49π

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Surcface area of cylindrical tunnel = 2πrh
   

   =		2 × π ×	5	× 10		sq.metre
   			2

   
   = 50π sq.m.

   Correct Option: B

   Surcface area of cylindrical tunnel = 2πrh
   

   =		2 × π ×	5	× 10		sq.metre
   			2

   
   = 50π sq.m.

---

---

485. Let ABCDEF be a prism whose base is a right angled triangle, where sides adjacent to 90° are 9 cm and 12 cm. If the cost of painting the prism is Rs. 151.20, at the rate of 20 paise per sq cm then the height of the prism is :
     

1. 1. 17 cm
      

   
   
   

   2. 18 cm
      

   
   
   

   3. 15 cm
      

   
   
   

   4. 16 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Total surface area of prism =	151.2.	=	1215	= 756 sq.cm.
   	0.20		2

   
   Hypotenuse of the triangular base = √9² + 12² = √81 + 144
   = √225 = 15 cm.
   ∴ Perimeter of base = 9 + 12 + 15 = 36 cm.
   ∴ Total surface area = Perimeter of base × height + 2 × area of base
   

   ⇒ 756 = 36 × h + 2 ×	1	× 9 × 12
   	2

   
   →756 = 36h + 108
   ⇒ 36h = 756 – 108 = 648
   

   ⇒ h =	648	= 18 cm.
   	36

   Correct Option: B

   Total surface area of prism =	151.2.	=	1215	= 756 sq.cm.
   	0.20		2

   
   Hypotenuse of the triangular base = √9² + 12² = √81 + 144
   = √225 = 15 cm.
   ∴ Perimeter of base = 9 + 12 + 15 = 36 cm.
   ∴ Total surface area = Perimeter of base × height + 2 × area of base
   

   ⇒ 756 = 36 × h + 2 ×	1	× 9 × 12
   	2

   
   →756 = 36h + 108
   ⇒ 36h = 756 – 108 = 648
   

   ⇒ h =	648	= 18 cm.
   	36

---