Mensuration
- If one diagonal of a rhombus of side 13 cm is 10 cm, then the other diagonal is
-
View Hint View Answer Discuss in Forum
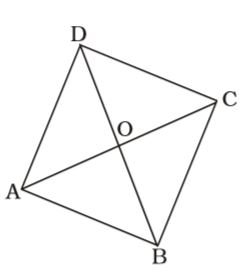
AC = 10 cm. AO = OC = 5 cm.
∠ AOB = 90° AB = 13 cm.
From ∆AOB,
∴ OB = √AB² - OA²
= √13² + 5² = √169 - 25
= √144 = 12 cm.
∴ BD = 2OB = 2 × 12 = 24 cm.Correct Option: A

AC = 10 cm. AO = OC = 5 cm.
∠ AOB = 90° AB = 13 cm.
From ∆AOB,
∴ OB = √AB² - OA²
= √13² + 5² = √169 - 25
= √144 = 12 cm.
∴ BD = 2OB = 2 × 12 = 24 cm.
- A brick 2" thick is placed against a wheel to act for a stop. The horizontal distance of the face of the brick from the point where the wheel touches the ground is 6". The radius of the wheel in inches is
-
View Hint View Answer Discuss in Forum

BC = 2" ; ∠ ODB = 90°
BD = 6" = Radius of wheelCorrect Option: D

BC = 2" ; ∠ ODB = 90°
BD = 6" = Radius of wheel
- A solid has 12 vertices and 30 edges. How many faces does it have?
-
View Hint View Answer Discuss in Forum
According to the Euler’s formula, V + F – E = 2
⇒ 12 + F – 30 = 2
⇒ F – 18 = 2
⇒ F = 18 + 2 = 20Correct Option: D
According to the Euler’s formula, V + F – E = 2
⇒ 12 + F – 30 = 2
⇒ F – 18 = 2
⇒ F = 18 + 2 = 20
- A sphere of radius r is inscribed in a right circular cone whose slant height equals twice the radius of the base a. What is the relation between r and a ?
-
View Hint View Answer Discuss in Forum

AB = 2a
BD = a
AD = √4a² - a²
= √3a² = √3a
= ∠AFO = 90°
OD = r
AO = √3a - rsin BAD = a = 1 2a 2
∠BAD = 30°
sin30°= OF ⇒ 1 = r = r OA 2 OA √3a - r
⇒ 2r = √3a - r
⇒ 3r = √3a⇒ a √3 Correct Option: C

AB = 2a
BD = a
AD = √4a² - a²
= √3a² = √3a
= ∠AFO = 90°
OD = r
AO = √3a - rsin BAD = a = 1 2a 2
∠BAD = 30°
sin30°= OF ⇒ 1 = r = r OA 2 OA √3a - r
⇒ 2r = √3a - r
⇒ 3r = √3a⇒ a √3
- When the length of rectangle is decreased by 10ft. and the breadth is increased by 5 feet, the rectangle becomes a square and its area is reduced by 210 square feet. Find the area of the rectangle.
-
View Hint View Answer Discuss in Forum
Let the length and breadth of rectangle be x and y feet respectively.
Area of rectangle = xy
Again, x – 10 = y + 5 = side of square
⇒ x = y + 15 ....(i)
Again, xy – (y + 5)² = 210
⇒ y (y + 15) – (y² + 10y + 25) = 210
⇒ y² + 15y – y² – 10y – 25 = 210
⇒ 5y = 235
⇒ y = 47 feet
∴ x = y + 5 = 52 feet
Area of rectangle = 52 × 47 = 2444 sq. feetCorrect Option: C
Let the length and breadth of rectangle be x and y feet respectively.
Area of rectangle = xy
Again, x – 10 = y + 5 = side of square
⇒ x = y + 15 ....(i)
Again, xy – (y + 5)² = 210
⇒ y (y + 15) – (y² + 10y + 25) = 210
⇒ y² + 15y – y² – 10y – 25 = 210
⇒ 5y = 235
⇒ y = 47 feet
∴ x = y + 5 = 52 feet
Area of rectangle = 52 × 47 = 2444 sq. feet

