666. In an equilateral triangle of side 24 cm., a circle is inscribed touching its sides. The area of the remaining portion of the triangle is approximately equal to assuming π = 22/7 & √3 = 1.732
     

1. 1. 36.6 cm²
      

   
   
   

   2. 54.2 cm²
      

   
   
   

   3. 72.8 cm²
      

   
   
   

   4. 98.5 cm²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

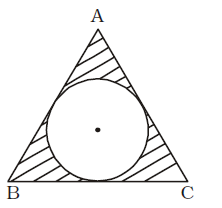
   Radius of circle =	a
   	2√3

   
   

   =	24	= 4√3 cm
   	2√3

   
   ∴ Area of circle = π (4√3)²
   = 48π sq. cm.
   

   =		48 ×	22		sq. cm
   			7

   
   = 150.86 sq. cm.
   

   Area of ∆ABC =		√3	× 24 × 24		sq. cm
   		4

   
   = 144 × 1.732
   = 249.408 sq. cm.
   ∴ Area of the shaded region
   = (249.408 – 150.86) sq. cm.
   = 98.548 sq. cm.

   Correct Option: D

   
   

   Radius of circle =	a
   	2√3

   
   

   =	24	= 4√3 cm
   	2√3

   
   ∴ Area of circle = π (4√3)²
   = 48π sq. cm.
   

   =		48 ×	22		sq. cm
   			7

   
   = 150.86 sq. cm.
   

   Area of ∆ABC =		√3	× 24 × 24		sq. cm
   		4

   
   = 144 × 1.732
   = 249.408 sq. cm.
   ∴ Area of the shaded region
   = (249.408 – 150.86) sq. cm.
   = 98.548 sq. cm.

---

667. The inradius of triangle is 4 cm and its area is 34 sq. cm. the perimeter of the triangle is :
     

1. 1. 8.5 cm
      

   
   
   

   2. 17 cm
      

   
   
   

   3. 34 cm
      

   
   
   

   4. 20 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   In-radius =	Area
   	Semi - perimeter

   
   

   ⇒ 4 =	34
   	Semi - perimeter

   
   

   ⇒ Semi - perimeter =	34	= 8.5
   	4

   
   ∴ Perimeter of triangle = (8.5 × 2) cm = 17 cm

   Correct Option: B

   In-radius =	Area
   	Semi - perimeter

   
   

   ⇒ 4 =	34
   	Semi - perimeter

   
   

   ⇒ Semi - perimeter =	34	= 8.5
   	4

   
   ∴ Perimeter of triangle = (8.5 × 2) cm = 17 cm

---

---

668. The area of a triangle ABC is 10.8 cm². If CP = PB and 2AQ = QB, then the area of the triangle APQ is
     

1. 1. 3.6 cm²
      

   
   
   

   2. 0.9 cm²
      

   
   
   

   3. 2.7 cm²
      

   
   
   

   4. 1.8 cm²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
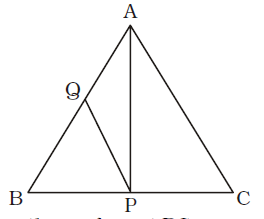
   AP is the median at BC.
   ∴ Area of ∆ABP = Area of ∆APC
   Again, 2AQ = QB
   

   ∴ Area of ∆APQ =	1	Area of ∆ABP
   	3

   
   

   ∴ Area of ∆APQ =	1	Area of ∆ABC
   	6

   
   

   =		1	× 10.8		sq. cm
   		6

   
   = 1.8 sq.cm.

   Correct Option: D

   
   AP is the median at BC.
   ∴ Area of ∆ABP = Area of ∆APC
   Again, 2AQ = QB
   

   ∴ Area of ∆APQ =	1	Area of ∆ABP
   	3

   
   

   ∴ Area of ∆APQ =	1	Area of ∆ABC
   	6

   
   

   =		1	× 10.8		sq. cm
   		6

   
   = 1.8 sq.cm.

---

669. If a circle of radius 12 cm is divided into two equal parts by one concentric circle, then radius of inner circle is :
     

1. 1. 6 cm
      

   
   
   

   2. 4 cm
      

   
   
   

   3. 6√2 cm
      

   
   
   

   4. 4√2 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
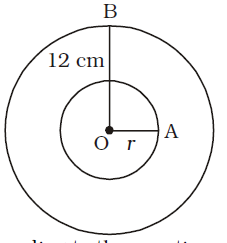
   According to the question,
   π × 12² = 2πr²
   ⇒ 2r² = 12 × 12
   

   ⇒ r² =	12 × 12	= 72
   	2

   
   ⇒ r = √72 = 6√2 cm.

   Correct Option: C

   
   According to the question,
   π × 12² = 2πr²
   ⇒ 2r² = 12 × 12
   

   ⇒ r² =	12 × 12	= 72
   	2

   
   ⇒ r = √72 = 6√2 cm.

---

---

670. In ∆ABC, the medians AD and BE meet at G. The ratio of the areas of ∆BDG and the quadrilateral GDCE is :
     

1. 1. 1 : 2
      

   
   
   

   2. 1 : 3
      

   
   
   

   3. 2 : 3
      

   
   
   

   4. 3 : 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
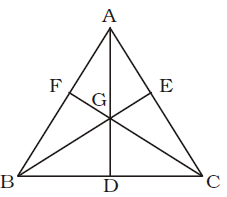
   Area of ∆ABD = Area of ∆ADC = Area of ∆BCE
   Clearly,
   Area of ∆BDG = Area of ∆CGD = Area of ∆CEG
   ∆BDG : ∎ GDCE = 1 : 2

   Correct Option: A

   
   Area of ∆ABD = Area of ∆ADC = Area of ∆BCE
   Clearly,
   Area of ∆BDG = Area of ∆CGD = Area of ∆CEG
   ∆BDG : ∎ GDCE = 1 : 2

---