Mensuration
- The diagonals of two squares are in the ratio of 3 : 7. What is the ratio of their areas?
-
View Hint View Answer Discuss in Forum
Area of square = 1 × (diagonal)² 2 ∴ Required ratio = d1² d2² = 
3 
² = 9 = 9 : 49 7 79 Correct Option: B
Area of square = 1 × (diagonal)² 2 ∴ Required ratio = d1² d2² = 
3 
² = 9 = 9 : 49 7 79
- A string of length 24 cm is bent first into a square and then into a right–angled triangle by keeping one side of the square fixed as its base. Then the area of triangle equals to :
-
View Hint View Answer Discuss in Forum
Side of square = 24 cm. = 6 cm. 4
Base of triangle = 6 cm.
∵ 6² + 8² = 10² and 6 + 8 + 10 = 24
∴ Height of triangle = 8 cm.∴ Area of triangle = 1 × 6 × 8 = 24 sq. cm. 2 Correct Option: A
Side of square = 24 cm. = 6 cm. 4
Base of triangle = 6 cm.
∵ 6² + 8² = 10² and 6 + 8 + 10 = 24
∴ Height of triangle = 8 cm.∴ Area of triangle = 1 × 6 × 8 = 24 sq. cm. 2
- ABCD is a square. Draw an equilateral triangle PBC on side BC considering BC is a base and an equilateral triangle QAC on diagonal AC considering AC is a base. Find the value of
Area of ∆PBC Area ∆QAC
-
View Hint View Answer Discuss in Forum
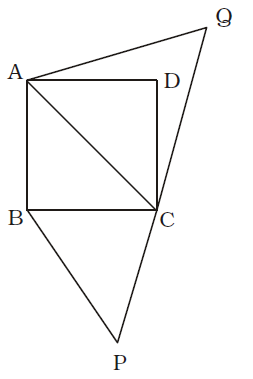
Side of square = x units
Diagonal of square = √2x units∴ Area of ∆PBC = √3 x² Area of ∆QAC 4 √3 (√2x)² 4
= 1/2Correct Option: A

Side of square = x units
Diagonal of square = √2x units∴ Area of ∆PBC = √3 x² Area of ∆QAC 4 √3 (√2x)² 4
= 1/2
- The area of a rectangle is 60 cm² and its perimeter is 34 cm, then the length of the diagonal is
-
View Hint View Answer Discuss in Forum
Let the length of rectangle be a cm and its breadth be b cm.
According to the question,
Area of rectangle = ab = 60 ... (i)
and, perimeter of rectangle = 2 (a + b)
⇒ 2 (a + b) = 34
= a + b = 17
On squaring both sides,
a² + b² + 2ab = 172 = 289
⇒ a² + b² + 2 × 60 = 289
[From equation (i)]
⇒ a² + b² = 289 – 120 = 169
∴ Diagonal of rectangle = √a² + b² = √169
= 13 cm.Correct Option: D
Let the length of rectangle be a cm and its breadth be b cm.
According to the question,
Area of rectangle = ab = 60 ... (i)
and, perimeter of rectangle = 2 (a + b)
⇒ 2 (a + b) = 34
= a + b = 17
On squaring both sides,
a² + b² + 2ab = 172 = 289
⇒ a² + b² + 2 × 60 = 289
[From equation (i)]
⇒ a² + b² = 289 – 120 = 169
∴ Diagonal of rectangle = √a² + b² = √169
= 13 cm.
- The centroid of a triangle ∆ABC is G. If the area of ∆ABC = 72 sq. units , then the area of ∆BGC is
-
View Hint View Answer Discuss in Forum
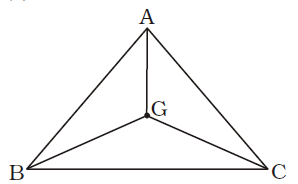
Point G is the centroid of ∆ABC.
∴ ∆BGC ≅ ∆AGC ≅ AGB∴ Area of ∆BGC = 1 × 72 × = 24 sq. units 3 Correct Option: B

Point G is the centroid of ∆ABC.
∴ ∆BGC ≅ ∆AGC ≅ AGB∴ Area of ∆BGC = 1 × 72 × = 24 sq. units 3

