16. The diagonal of a square A is (a+b). The diagonal of a square whose area is twice the area of square A, is
    

1. 1. 2 (a+b)
      

   
   
   

   2. 2 (a+b)²
      

   
   
   

   3. √2(a+b)
      

   
   
   

   4. √2(a-b)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 10,
   

   Area of the square A =	(diagonal)²
   	2

   
   

   =	(a + b)²
   	2

   
   

   Area of the new square =	(a + b)²	× 2 = (a + b)²
   	2

   
   ⇒ Side = (a + b)
   ∴ Diagonal = √2 × side = √2 (a + b)

   Correct Option: C

   Using Rule 10,
   

   Area of the square A =	(diagonal)²
   	2

   
   

   =	(a + b)²
   	2

   
   

   Area of the new square =	(a + b)²	× 2 = (a + b)²
   	2

   
   ⇒ Side = (a + b)
   ∴ Diagonal = √2 × side = √2 (a + b)

---

17. The diagonal of a square is 4√2 cm. The diagonal of another square whose area is double that of the first square is :
    

1. 1. 8√2 cm
      

   
   
   

   2. 16 cm
      

   
   
   

   3. √32 cm
      

   
   
   

   4. 8 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 10, Side of the first square
   

   =	1	× 4√2 = 4cm
   	√2

   
   Its area = (4)² = 16 cm².
   ∴ Area of second square = 2 × 16 = 32 cm².
   Its side = √32 = 4 √2cm.
   ∴ Required diagonal = √2 × 4√2 = 8 cm

   Correct Option: D

   Using Rule 10, Side of the first square
   

   =	1	× 4√2 = 4cm
   	√2

   
   Its area = (4)² = 16 cm².
   ∴ Area of second square = 2 × 16 = 32 cm².
   Its side = √32 = 4 √2cm.
   ∴ Required diagonal = √2 × 4√2 = 8 cm

---

---

18. If the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
    

1. 1. 15.12 sq.cm
      

   
   
   

   2. 13.52 sq.cm
      

   
   
   

   3. 12.62 sq.cm
      

   
   
   

   4. 10.00 sq.cm.

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 10,
   

   Side of square =	Diagonal
   	√2

   
   

   ∴ Area =	(Diagonal)²
   	2

   
   

   =	(5.2)²	=	27.04	= 13.52cm²
   	2		2

   Correct Option: B

   Using Rule 10,
   

   Side of square =	Diagonal
   	√2

   
   

   ∴ Area =	(Diagonal)²
   	2

   
   

   =	(5.2)²	=	27.04	= 13.52cm²
   	2		2

---

19. The area of a rectangle is thrice that of a square. The length of the rectangle is 20 cm and the breadth of the rectangle is 3/2 times that of the side of the square. The side of the square, (in cm) is
    

1. 1. 10
      

   
   
   

   2. 20
      

   
   
   

   3. 30
      

   
   
   

   4. 60

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 9 and 10,
   Side of a square = x cm
   ∴ Area of rectangle = 3 × area of square
   

   ⇒ 20 ×	3	x = 3 × x²
   	2

   
   

   ⇒ x =	20 × 3	= 10 cm
   	2 × 3

   Correct Option: A

   Using Rule 9 and 10,
   Side of a square = x cm
   ∴ Area of rectangle = 3 × area of square
   

   ⇒ 20 ×	3	x = 3 × x²
   	2

   
   

   ⇒ x =	20 × 3	= 10 cm
   	2 × 3

---

---

20. In an isosceles triangle, the measure of each of equal sides is 10 cm and the angle between them is 45°. the area of the triangle is
    

1. 1. 25 cm²
      

   
   
   

   2. 25	√2cm²
      2

      
      

   
   
   

   3. 25√2 cm²
      

   
   
   

   4. 25√3cm²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
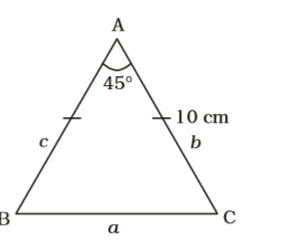
   AB = AC = 10 cm
   

   ∴ Area =	1	be in A
   	2

   
   

   =	1	× 10 × 10 × sin 45°
   	2

   
   

   =	50	=	50 × √2	= 25√2cm²
   	2		√2 × √2

   Correct Option: C

   
   AB = AC = 10 cm
   

   ∴ Area =	1	be in A
   	2

   
   

   =	1	× 10 × 10 × sin 45°
   	2

   
   

   =	50	=	50 × √2	= 25√2cm²
   	2		√2 × √2

---