Mensuration
- The area of a rhombus is 150 cm². The length of one of its diagonals is 10 cm. The length of the other diagonal is :
-
View Hint View Answer Discuss in Forum
Using Rule 12,
Let d1, d2 be the diagonals of a rhombus,Area = 1 d1.d2 2 ⇒ 150 = 1 × 10 × d2 2 ⇒ d2 = 150 = 30 cm 5 Correct Option: B
Using Rule 12,
Let d1, d2 be the diagonals of a rhombus,Area = 1 d1.d2 2 ⇒ 150 = 1 × 10 × d2 2 ⇒ d2 = 150 = 30 cm 5
- The perimeter of a rhombus is 100 cm. If one of its diagonals is 14 cm, then the area of the rhombus is
-
View Hint View Answer Discuss in Forum
Using Rule 12,
Perimeter of rhombus
= 2 √d1² + d2²
Where d1 and d2 are diagonals.
∴ 2√d1² + d2² = 100
⇒ √d1² + d2² = 50
⇒ d1² + d2² = 2500
⇒ (14)² + d2² = 2500
⇒ d2² = 2500 – 196 = 2304
∴ d² = √2304 = 48∴ Area of the rhombus = 1 d1² × d2² 2 ∴ Area of the rhombus = 1 14 × 48 = 336 sq.cm 2 Correct Option: C
Using Rule 12,
Perimeter of rhombus
= 2 √d1² + d2²
Where d1 and d2 are diagonals.
∴ 2√d1² + d2² = 100
⇒ √d1² + d2² = 50
⇒ d1² + d2² = 2500
⇒ (14)² + d2² = 2500
⇒ d2² = 2500 – 196 = 2304
∴ d² = √2304 = 48∴ Area of the rhombus = 1 d1² × d2² 2 ∴ Area of the rhombus = 1 14 × 48 = 336 sq.cm 2
- If the measure of one side and one diagonal of a rhombus are 10 cm and 16 cm respectively, then its area (in cm²) is :
-
View Hint View Answer Discuss in Forum
Using Rule 12, A
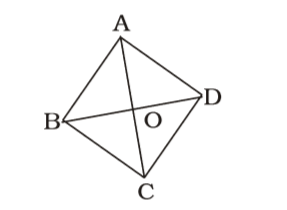
AB = 10cm,
AC = 16 cm;
⇒ AO = 8 cm
∴ BO = √10² - 8²
= √100 - 64 = √36 = 6 cm
∴ BD = 12cm
Hence,
Area of rhombus = d1d2= 1 × 16 × 12 = 96cm² 2 Correct Option: C
Using Rule 12, A

AB = 10cm,
AC = 16 cm;
⇒ AO = 8 cm
∴ BO = √10² - 8²
= √100 - 64 = √36 = 6 cm
∴ BD = 12cm
Hence,
Area of rhombus = d1d2= 1 × 16 × 12 = 96cm² 2
- The ratio of the length of the parallel sides of a trapezium is 3 : 2. The shortest distance between them is 15 cm. If the area of the trapezium is 450 cm², the sum of the length of the parallel sides is
-
View Hint View Answer Discuss in Forum
Using Rule 13,
Area of the trapezium = 1 (sum of parallel sides) × altitude 2 ⇒ 450 = 1 (3x + 2x) × 15 2 ⇒ 5x = 450 × 2 = 60cm 15 Correct Option: D
Using Rule 13,
Area of the trapezium = 1 (sum of parallel sides) × altitude 2 ⇒ 450 = 1 (3x + 2x) × 15 2 ⇒ 5x = 450 × 2 = 60cm 15
- The area of an equilateral triangle is 9√3m² . The length (in m) of the median is
-
View Hint View Answer Discuss in Forum
Using Rule 6,

√3 × side² = 9√3 4
⇒ Side² = 9 × 4 = 36
⇒ Side = √36 = 6 metre
∴ BD = 3 metre
AD = √AB² - BD² = √6² - 3²
= √36 - 9 = √27
= 3√3 metreCorrect Option: B
Using Rule 6,

√3 × side² = 9√3 4
⇒ Side² = 9 × 4 = 36
⇒ Side = √36 = 6 metre
∴ BD = 3 metre
AD = √AB² - BD² = √6² - 3²
= √36 - 9 = √27
= 3√3 metre

