Mensuration

Mensuration

Easy Questions
Moderate Questions
Difficult Questions

Aptitude

Simplification
Number System
Fractions
Elementary Algebra
LCM and HCF
Approximation
Unitary Method
Linear Equation
Quadratic Equation
Discount
Average
Surds and Indices
Percentage
Square root and cube root
Order of Magnitude
Work and Wages
Odd Man Out and Series
Algebra
Profit and Loss
Stocks and Shares
True Discount
Ratio, Proportion
Partnership
Alligation or Mixture
Time and Work
Pipes and Cistern
Speed, Time and Distance
Problem on Trains
Height and Distance
Banker's Discount
Boats and Streams
Races and games
Problems on Ages
Clocks and Calendars
Simple interest
Compound Interest
Sets and Functions
Area and Perimeter
Volume and Surface Area of Solid Figures
Sequences and Series
Plane Geometry
Logarithm
Probability
Permutation and Combination
Statistics
Mensuration
Trigonometry
Aptitude miscellaneous
  1. Two adjacent sides of a parallelogram are of length 15 cm and 18 cm. If the distance between two smaller sides is 12 cm, then the distance between two bigger sides is








  1. View Hint View Answer Discuss in Forum

    Area of the parallelogram = Base × Height
    = 15 × 12 = 180 sq.cm.
    ∴ 180 = 18 × height
    ⇒ Height = 10 cm

    Correct Option: B

    Area of the parallelogram = Base × Height
    = 15 × 12 = 180 sq.cm.
    ∴ 180 = 18 × height
    ⇒ Height = 10 cm

  1. A parallelogram ABCD has sides AB = 24 cm and AD = 16 cm. The distance between the sides AB and DC is 10 cm. Find the distance between the sides AD and BC.








  1. View Hint View Answer Discuss in Forum


    Area of the parallelogram = Base × Height
    = 24 × 10 = 240 sq.cm.
    If the required distance be x cm, then
    240 = 16 × x

    ⇒ x =
    240
    		 = 15 cm
    16

    Correct Option: C


    Area of the parallelogram = Base × Height
    = 24 × 10 = 240 sq.cm.
    If the required distance be x cm, then
    240 = 16 × x

    ⇒ x =
    240
    		 = 15 cm
    16

  1. The adjacent sides of a parallelogram are 36 cm and 27 cm in length. If the distance between the shorter sides is 12 cm, then the distance between the longer sides is








  1. View Hint View Answer Discuss in Forum

    Area of parallelogram = base × height
    = 27 × 12 = 324 sq. cm.
    Again,
    324 = 36 × h

    ⇒ h =
    324
    		 = 9 cm
    36

    Correct Option: D

    Area of parallelogram = base × height
    = 27 × 12 = 324 sq. cm.
    Again,
    324 = 36 × h

    ⇒ h =
    324
    		 = 9 cm
    36

  1. If the diagonals of a rhombus are 8 and 6, then the square of its size is








  1. View Hint View Answer Discuss in Forum

    BO = 4 units; OC = 3 units
    ∠BOC = 90°

    ∴ BC = √4² + 3² = 5 units
    ∴ BC² = 25 sq. units

    Correct Option: A

    BO = 4 units; OC = 3 units
    ∠BOC = 90°

    ∴ BC = √4² + 3² = 5 units
    ∴ BC² = 25 sq. units

  1. One of the four angles of a rhombus is 60°. If the length of each side of the rhombus is 8 cm, then the length of the longer diagonal is








  1. View Hint View Answer Discuss in Forum


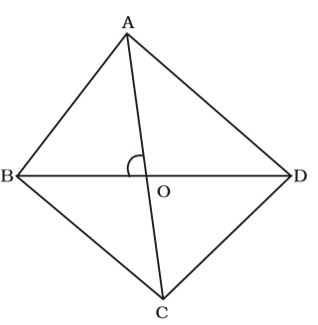
    ∠BAD = 60°
    ∴ ∠BAO = 30° ∠ABO = 60°

    ∴ sin 60° =
    OA
    AB

    ⇒
    √3
    		 × 8 = OA
    2

    ⇒ OA = 4√3
    ∴ AC = 8√3 cm

    Correct Option: A


    ∠BAD = 60°
    ∴ ∠BAO = 30° ∠ABO = 60°

    ∴ sin 60° =
    OA
    AB

    ⇒
    √3
    		 × 8 = OA
    2

    ⇒ OA = 4√3
    ∴ AC = 8√3 cm