Mensuration

Mensuration

Easy Questions
Moderate Questions
Difficult Questions

Aptitude

Simplification
Number System
Fractions
Elementary Algebra
LCM and HCF
Approximation
Unitary Method
Linear Equation
Quadratic Equation
Discount
Average
Surds and Indices
Percentage
Square root and cube root
Order of Magnitude
Work and Wages
Odd Man Out and Series
Algebra
Profit and Loss
Stocks and Shares
True Discount
Ratio, Proportion
Partnership
Alligation or Mixture
Time and Work
Pipes and Cistern
Speed, Time and Distance
Problem on Trains
Height and Distance
Banker's Discount
Boats and Streams
Races and games
Problems on Ages
Clocks and Calendars
Simple interest
Compound Interest
Sets and Functions
Area and Perimeter
Volume and Surface Area of Solid Figures
Sequences and Series
Plane Geometry
Logarithm
Probability
Permutation and Combination
Statistics
Mensuration
Trigonometry
Aptitude miscellaneous
  1. The ratio of the area of the in-circle and the circum-circle of a square is








  1. View Hint View Answer Discuss in Forum

    Using Rule 14,

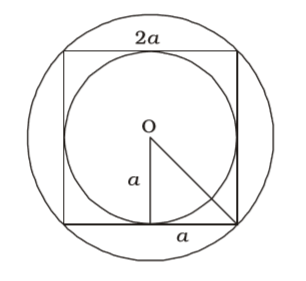
    Let the side of the square be 2x. Then radius of incircle = a Radius of circum-circle
    √a² + a² = √2a
    ∴ Ratio of area = πa² : π(√2a)² = a² : 2a² = 1 : 2

    Correct Option: A

    Using Rule 14,

    Let the side of the square be 2x. Then radius of incircle = a Radius of circum-circle
    √a² + a² = √2a
    ∴ Ratio of area = πa² : π(√2a)² = a² : 2a² = 1 : 2

  1. The perimeter of a semicircular path is 36 m. Find the area of this semicircular path.








  1. View Hint View Answer Discuss in Forum

    Using Rule 14,
    πr + 2r = 36

    ⇒ r
    22
    		 + 2 = 36
    7

    ⇒ r
    22 + 14
    		 = 36
    7

    ⇒ r =
    36 × 7
    		 = 7 metre
    36

    Area =
    πr²
    2

    =
    1
    		 ×
    22
    		 × 7 × 7
    27

    = 77 sq. metre

    Correct Option: D

    Using Rule 14,
    πr + 2r = 36

    ⇒ r
    22
    		 + 2 = 36
    7

    ⇒ r
    22 + 14
    		 = 36
    7

    ⇒ r =
    36 × 7
    		 = 7 metre
    36

    Area =
    πr²
    2

    =
    1
    		 ×
    22
    		 × 7 × 7
    27

    = 77 sq. metre

  1. The ratio between the area of two circles is 4 : 7. What will be the ratio of their radii?








  1. View Hint View Answer Discuss in Forum

    Using Rule 14,
    πr1² : π2² = 4 : 7
    ⇒ r1 : r2 : √4 : √7 = 2 : √7

    Correct Option: A

    Using Rule 14,
    πr1² : π2² = 4 : 7
    ⇒ r1 : r2 : √4 : √7 = 2 : √7

  1. Three circles of radius a, b, c touch each other externally. The area of the triangle formed by joining their centre is








  1. View Hint View Answer Discuss in Forum

    Using Rule 1,

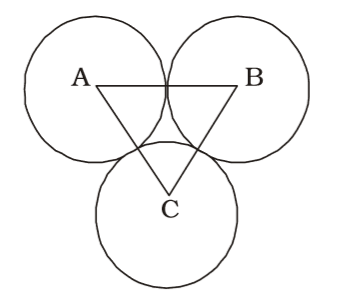
    x = AB = a + b
    y = BC = b + c
    z = CA = a + c

    ∴ s =
    AB + BC + CA
    		 = a + b + c
    2

    ∴ Area of ∆ ABC
    = √s(s - x)(s - y)(s - z)
    = √(a + b + c)abc

    Correct Option: A

    Using Rule 1,

    x = AB = a + b
    y = BC = b + c
    z = CA = a + c

    ∴ s =
    AB + BC + CA
    		 = a + b + c
    2

    ∴ Area of ∆ ABC
    = √s(s - x)(s - y)(s - z)
    = √(a + b + c)abc

  1. The area of a circle is proportional to the square of its radius. A small circle of radius 3 cm is drawn within a larger circle of radius 5 cm. Find the ratio of the area of the annular zone to the area of the larger circle. (Area of the annular zone is the difference between the area of the larger circle and that of the smaller circle).








  1. View Hint View Answer Discuss in Forum

    Using Rule 14,

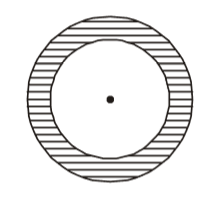
    Area of circle = kr²
    Area of shaded region
    = k (5² – 3²) = 16π sq. units
    Area of larger circle = k × 5²
    = 25p sq. units
    ∴ Required ratio = 16 : 25

    Correct Option: C

    Using Rule 14,

    Area of circle = kr²
    Area of shaded region
    = k (5² – 3²) = 16π sq. units
    Area of larger circle = k × 5²
    = 25p sq. units
    ∴ Required ratio = 16 : 25