301. A chord of length 30 cm is at a distance of 8 cm from the centre of a circle. The radius of the circle is:
     

1. 1. 17 cm
      

   
   
   

   2. 23 cm
      

   
   
   

   3. 21 cm
      

   
   
   

   4. 19 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   AD = DB = 15 cm[∵AB = 30 cm]
   OD = 8 cm
   OA = √15² + 8² = √225 + 64
   = √289 = 17cm

   Correct Option: A

   
   AD = DB = 15 cm[∵AB = 30 cm]
   OD = 8 cm
   OA = √15² + 8² = √225 + 64
   = √289 = 17cm

---

302. The circum-radius of an equilateral triangle is 8 cm. The in-radius of the triangle is
     

1. 1. 3.25 cm
      

   
   
   

   2. 3.50 cm
      

   
   
   

   3. 4 cm
      

   
   
   

   4. 4.25 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

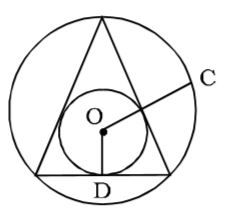
   ∵	OC	=	2
   	OD		1

   
   

   ⇒	8	=	2	⇒ OD = 4 cm.
   	OD		1

   
   In-radius = 4 cm

   Correct Option: C

   
   

   ∵	OC	=	2
   	OD		1

   
   

   ⇒	8	=	2	⇒ OD = 4 cm.
   	OD		1

   
   In-radius = 4 cm

---

---

303. An inverted conical shaped vessel is filled with water to its brim. The height of the vessel is 8 cm and radius of the open end is 5 cm. When a few solid spherical metallic balls each of radius 1/2 cm are dropped in the vessel, 25% water is overflowed. The number of balls is :
     

1. 1. 100
      

   
   
   

   2. 400
      

   
   
   

   3. 200
      

   
   
   

   4. 150

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volume of concial vessel =	1	πr²h
   	3

   
   

   =	1	π × (5)² × 8
   	3

   
   

   =	200π	cu.cm. = Volume of water
   	3

   
   

   Volume of 25% of water =	1	×	200π	=	50π	cu.cm.
   	4		3		3

   
   

   Volume of ball =	4	πR³
   	3

   
   

   =	4	π ×		1		³	cu.cm.
   	3			2

   
   

   =	π	cu.cm.
   	6

   
   

   ∴ Number of balls =	50π	=
   	3		50π	×	6	= 100
   	π		3		π
   	6

   Correct Option: A

   Volume of concial vessel =	1	πr²h
   	3

   
   

   =	1	π × (5)² × 8
   	3

   
   

   =	200π	cu.cm. = Volume of water
   	3

   
   

   Volume of 25% of water =	1	×	200π	=	50π	cu.cm.
   	4		3		3

   
   

   Volume of ball =	4	πR³
   	3

   
   

   =	4	π ×		1		³	cu.cm.
   	3			2

   
   

   =	π	cu.cm.
   	6

   
   

   ∴ Number of balls =	50π	=
   	3		50π	×	6	= 100
   	π		3		π
   	6

---

304. If the area of the base of a cone is increased by 100%, then the volume increases by
     

1. 1. 200%
      

   
   
   

   2. 182%
      

   
   
   

   3. 141%
      

   
   
   

   4. 100%

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 10,
   Increase in height = 0%
   

   Volume =	1	area of base × height
   	3

   
   

   ∴ Percentage increase =		x + y +	xy		%
   			100

   
   

   =		100 + 0 +	100 × 0		% = 100%
   			100

   Correct Option: D

   Using Rule 10,
   Increase in height = 0%
   

   Volume =	1	area of base × height
   	3

   
   

   ∴ Percentage increase =		x + y +	xy		%
   			100

   
   

   =		100 + 0 +	100 × 0		% = 100%
   			100

---

---

305. The percentage increase in the surface area of a cube when each side is doubled is
     

1. 1. 50%
      

   
   
   

   2. 200%
      

   
   
   

   3. 150%
      

   
   
   

   4. 300%

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 10,
   Required percentage increase
   

   Required percentage increase =		x + y +	xy		%
   			100

   
   

   =		100 + 100 +	100 × 100		% = 300%
   			100

   Correct Option: D

   Using Rule 10,
   Required percentage increase
   

   Required percentage increase =		x + y +	xy		%
   			100

   
   

   =		100 + 100 +	100 × 100		% = 300%
   			100

---