Mensuration
- If the arcs of square length in two circles subtend angles of 60° and 75° at their centres, the ratio of their radii is
-
View Hint View Answer Discuss in Forum
θ = s r
⇒ s = rθ
⇒ s = r1θ1 = r2θ2⇒ r1 = θ2 = 75 = 5 or 5 : 4 r2 θ2 60 4 Correct Option: C
θ = s r
⇒ s = rθ
⇒ s = r1θ1 = r2θ2⇒ r1 = θ2 = 75 = 5 or 5 : 4 r2 θ2 60 4
- The length of the perpendiculars drawn from any point in the interior of an equilateral triangle to the respective sides are p1, p2 and p3. The length of each side of the triangle is
-
View Hint View Answer Discuss in Forum
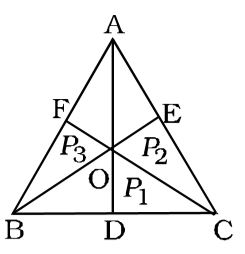
Let the side of ∆ABC be x.
O is the point in the interior of ∆ABC.
OD, OE, OF are perpendiculars.
∴ Clearly
∆OAB + ∆OBC + ∆OAC = ∆ABC⇒ 1 x × p3 + 1 x &yimes; p1 + 1 x &yimes; p2 = √3 x² 2 2 2 4 ⇒ 1 x(p3 + p1 + p2) = √3 x² 2 4 ⇒ p1 + p2 + p3 = √3 x 2 ⇒ x = 2 (p1 + p2 + p3) √3 Correct Option: A

Let the side of ∆ABC be x.
O is the point in the interior of ∆ABC.
OD, OE, OF are perpendiculars.
∴ Clearly
∆OAB + ∆OBC + ∆OAC = ∆ABC⇒ 1 x × p3 + 1 x &yimes; p1 + 1 x &yimes; p2 = √3 x² 2 2 2 4 ⇒ 1 x(p3 + p1 + p2) = √3 x² 2 4 ⇒ p1 + p2 + p3 = √3 x 2 ⇒ x = 2 (p1 + p2 + p3) √3
- The sides of a triangle are in the ratio 3 : 4 : 5. The measure of the largest angle of the triangle is
-
View Hint View Answer Discuss in Forum
Let the sides of triangle be 3x, 4x and 5x. Here,
(3x)² + (4x)² = (5x)²
∴ The triangle is right angled. Hence, the largest angle = 90°Correct Option: B
Let the sides of triangle be 3x, 4x and 5x. Here,
(3x)² + (4x)² = (5x)²
∴ The triangle is right angled. Hence, the largest angle = 90°
- From a point within an equilateral triangle, perpendiculars drawn to the three sides, are 6 cm, 7 cm and 8 cm respectively. the length of the side of the triangle is :
-
View Hint View Answer Discuss in Forum
Let ABC be equilateral triangle of side a cm and P be a point inside it.
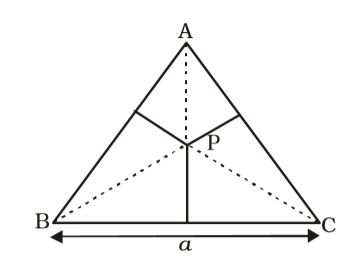
From the figure, Area of ∆APB + Area of ∆PBC + Area of ∆APC = Area of ∆ABC⇒ 1 × a × 6 + 1 × a × 7 + 1 × a × 8 = √3 a² 2 2 2 4 ⇒ 1 a (6 + 7 + 8) = √3 a² 2 4 ⇒ 21a = √3 a² 2 4 ⇒ a = 21 × 4 = 14√3 cm. 2 √3 Correct Option: C
Let ABC be equilateral triangle of side a cm and P be a point inside it.

From the figure, Area of ∆APB + Area of ∆PBC + Area of ∆APC = Area of ∆ABC⇒ 1 × a × 6 + 1 × a × 7 + 1 × a × 8 = √3 a² 2 2 2 4 ⇒ 1 a (6 + 7 + 8) = √3 a² 2 4 ⇒ 21a = √3 a² 2 4 ⇒ a = 21 × 4 = 14√3 cm. 2 √3
- The base and altitude of a right angled triangle are 12 cm and 5 cm respectively. The perpendicular distance of its hypotenuse from the opposite vertex is
-
View Hint View Answer Discuss in Forum
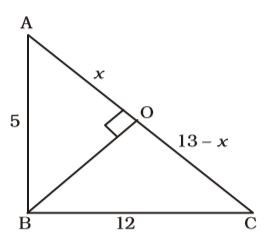
In ∆ABC,
AC = √12² + 5² = √144 + 25
= √169 = 13
Let AO = x. Then
OC = 13 – x
OB² = 5² – x² = 25 – x² ....(i)
OB² = 12² – (13 – x)²
= 144 – 169 – x2 + 26x ....(ii)
From (i) and (ii),
25 – x² = –25 – x² + 26x
→ 26x = 50⇒ x = 50 = 25 26 13
∴ OB² = 25 – x²= 25 - 
25 
² 13 ∴ OB² = 25 – x² = 25 – 
25 
² 13 OB² = 25 
1 - 25 
= 25 × 144 169 169 OB = √ 25 × 144 = 5 × 12 = 60 = 4 8 cm 169 13 13 13 Correct Option: B

In ∆ABC,
AC = √12² + 5² = √144 + 25
= √169 = 13
Let AO = x. Then
OC = 13 – x
OB² = 5² – x² = 25 – x² ....(i)
OB² = 12² – (13 – x)²
= 144 – 169 – x2 + 26x ....(ii)
From (i) and (ii),
25 – x² = –25 – x² + 26x
→ 26x = 50⇒ x = 50 = 25 26 13
∴ OB² = 25 – x²= 25 - 
25 
² 13 ∴ OB² = 25 – x² = 25 – 
25 
² 13 OB² = 25 
1 - 25 
= 25 × 144 169 169 OB = √ 25 × 144 = 5 × 12 = 60 = 4 8 cm 169 13 13 13

