The length of the perpendiculars drawn from any point in

Home » Aptitude » Mensuration » Question

The length of the perpendiculars drawn from any point in the interior of an equilateral triangle to the respective sides are p₁, p₂ and p₃. The length of each side of the triangle is

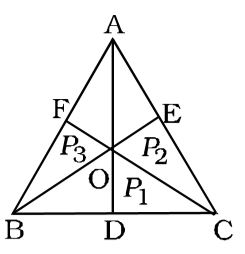
Let the side of ∆ABC be x.
O is the point in the interior of ∆ABC.
OD, OE, OF are perpendiculars.
∴ Clearly
∆OAB + ∆OBC + ∆OAC = ∆ABC

⇒	1	x × p₃ +	1	x &yimes; p₁ +	1	x &yimes; p₂ =	√3	x²
	2		2		2		4

⇒	1	x(p₃ + p₁ + p₂) =	√3	x²
	2		4

⇒ p₁ + p₂ + p₃ =	√3	x
	2

⇒ x =	2	(p₁ + p₂ + p₃)
	√3