-
The base and altitude of a right angled triangle are 12 cm and 5 cm respectively. The perpendicular distance of its hypotenuse from the opposite vertex is
-
-
4 4 cm 13
-
4 8 cm 13 - 5 cm
- 7 cm
-
Correct Option: B
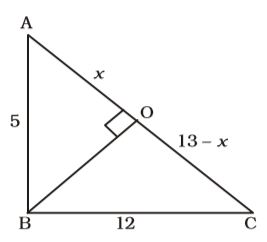
In ∆ABC,
AC = √12² + 5² = √144 + 25
= √169 = 13
Let AO = x. Then
OC = 13 – x
OB² = 5² – x² = 25 – x² ....(i)
OB² = 12² – (13 – x)²
= 144 – 169 – x2 + 26x ....(ii)
From (i) and (ii),
25 – x² = –25 – x² + 26x
→ 26x = 50
| ⇒ x = | = | ||
| 26 | 13 |
∴ OB² = 25 – x²
| = 25 - |  | 25 |  | ² |
| 13 |
| ∴ OB² = 25 – x² = 25 – |  | 25 |  | ² |
| 13 |
| OB² = 25 |  | 1 - |  | = 25 × | ||
| 169 | 169 |
| OB = √ | = | = | = 4 | cm | ||||
| 169 | 13 | 13 | 13 |

