Mensuration
- The area of a circular garden is 2464 sq.m. How much distance will have to be covered if you like to cross the garden along its diameter ? (Use π = 22/7 )
-
View Hint View Answer Discuss in Forum
Using Rule 14,
∵ πr² = 2464sq.m.⇒ r² = 2464 × 7 = 784 22
⇒ r = 28 m.
∴ Required distance = 2r = 2 × 28 = 56 metresCorrect Option: A
Using Rule 14,
∵ πr² = 2464sq.m.⇒ r² = 2464 × 7 = 784 22
⇒ r = 28 m.
∴ Required distance = 2r = 2 × 28 = 56 metres
- Four equal circles each of radius ‘a’ units touch one another. The area enclosed between them (π = 22/7 ), in square units, is
-
View Hint View Answer Discuss in Forum
Using Rule 10 and 14,
Area of shaded part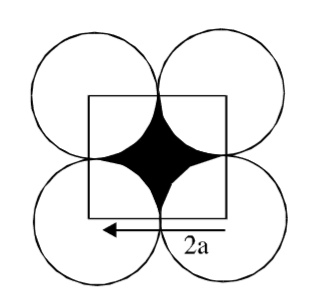
= Area of square – Area of circle= (2a)² - πr² = 4a² - 22 a² 7 ⇒ 28a² - 22a² = 6a² 7 7 Correct Option: B
Using Rule 10 and 14,
Area of shaded part
= Area of square – Area of circle= (2a)² - πr² = 4a² - 22 a² 7 ⇒ 28a² - 22a² = 6a² 7 7
- Length of the perpendiculars from a point in the interior of an equilateral triangle on its sides are 3 cm, 4 cm and 5 cm. Area of the triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 6, A
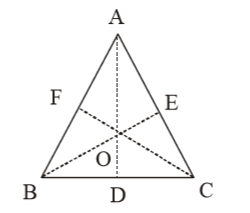
Let the side of the equilateral triangle be x cm.
∴ ∆AOB + ∆BOC + ∆COA = ∆ABC⇒ 1 x × 3 + 1 × x × 4 + 1 × x × 5 = √3 x² 2 2 2 4 ⇒ 6 = √3 x ⇒ x = 24 = 8√3 4 √3 ∴ Area of ∆ABC = √3 × side² 3 = √3 × 8√3 × 8√3 = 48√3sq. cm. 4 Correct Option: A
Using Rule 1 and 6, A

Let the side of the equilateral triangle be x cm.
∴ ∆AOB + ∆BOC + ∆COA = ∆ABC⇒ 1 x × 3 + 1 × x × 4 + 1 × x × 5 = √3 x² 2 2 2 4 ⇒ 6 = √3 x ⇒ x = 24 = 8√3 4 √3 ∴ Area of ∆ABC = √3 × side² 3 = √3 × 8√3 × 8√3 = 48√3sq. cm. 4
- The area of the largest triangle, that can be inscribed in a semicircle of radius r cm, is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
The largest triangle inscribed in a semi-circle will have base equal to 2r cm and height equal to r cm as shown in figure.
∴ Area = 1 × base × height 2 = 1 × 2r × r = r² cm² 2 Correct Option: B
Using Rule 1,
The largest triangle inscribed in a semi-circle will have base equal to 2r cm and height equal to r cm as shown in figure.
∴ Area = 1 × base × height 2 = 1 × 2r × r = r² cm² 2
- The area of the shaded region in the figure given below is
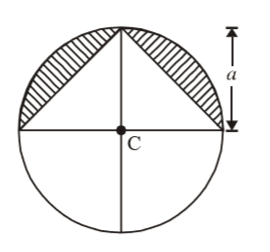
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 14,
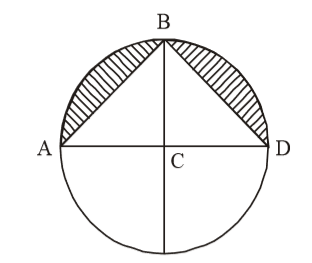
Let Radius of circle = a units \ Area of semi circle= πa² sq. units 2
Both triangles ∆ ABC and ∆ BCD are isosceles and equal.∴ Area of each triangle = 1 a² 2 ⇒ Area of both triangles = 2 × 1 a² = a² sq. units 2 ∴ Area of shaded region = πa² - a² = a² 
π - 1 
sq. units 2 2 Correct Option: C
Using Rule 1 and 14,

Let Radius of circle = a units \ Area of semi circle= πa² sq. units 2
Both triangles ∆ ABC and ∆ BCD are isosceles and equal.∴ Area of each triangle = 1 a² 2 ⇒ Area of both triangles = 2 × 1 a² = a² sq. units 2 ∴ Area of shaded region = πa² - a² = a² 
π - 1 
sq. units 2 2

