886. The area of a circle inscribed in a square of area 2m² is
     

1. 1. π	m²
      4

   
   
   

   2. π	m²
      2

   
   
   

   3. πm²
      

   
   
   

   4. 2πm²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 10 and 14,
   Side of square = √2 metre Radius of in-circle
   

   =	√2	=	1	metre
   	2		√2

   
   Area of the circle = πr²
   

   = π ×	1	=	π	sq. metre
   	2		2

   Correct Option: B

   Using Rule 10 and 14,
   Side of square = √2 metre Radius of in-circle
   

   =	√2	=	1	metre
   	2		√2

   
   Area of the circle = πr²
   

   = π ×	1	=	π	sq. metre
   	2		2

---

887. Three coins of the same size (radius 1 cm) are placed on a table such that each of them touches the other two. The area enclosed by the coins is

1. 1. 	π	- √3		cm²
      	2

   
   
   

   2. 	√3 -	π		cm²
      		2

   
   
   

   3. 	2√3 -	π		cm²
      		2

   
   
   

   4. 	3√3 -	π		cm²
      		2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 6 AND 17,
   
   Obviously, the triangle ABC will be equilateral.
   AB = BC = CA = 2 cm.
   Area of ∆ ABC
   

   =	√3	× 2 × 2
   	4

   
   = √3 cm²
   Then, area ‘A’ of the three sectors each of angle 60° in a circle of radius 1 cm.
   

   A = 3 ×	60	× π × 1 =	π
   	360		2

   
   ∴ Area of the shaded portion
   

   =		√3 -	π		cm².
   			2

   Correct Option: B

   Using Rule 6 AND 17,
   
   Obviously, the triangle ABC will be equilateral.
   AB = BC = CA = 2 cm.
   Area of ∆ ABC
   

   =	√3	× 2 × 2
   	4

   
   = √3 cm²
   Then, area ‘A’ of the three sectors each of angle 60° in a circle of radius 1 cm.
   

   A = 3 ×	60	× π × 1 =	π
   	360		2

   
   ∴ Area of the shaded portion
   

   =		√3 -	π		cm².
   			2

---

---

888. Each side of a regular hexagon is 1 cm. The area of the hexagon is
     

1. 1. 3√3	cm²
      2

      
      

   
   
   

   2. 3√3	cm²
      4

   
   
   

   3. 4√3 cm²
      

   
   
   

   4. 3√2 cm²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Area of regular hexagon =	3√3	× (side)²
   	2

   
   

   =	3√3	× 1 =	3√3	cm²
   	2		2

   Correct Option: A

   Area of regular hexagon =	3√3	× (side)²
   	2

   
   

   =	3√3	× 1 =	3√3	cm²
   	2		2

---

889. An equilateral triangle of side 6 cm has its corners cut off to form a regular hexagon. Area (in cm2) of this regular hexagon will be
     

1. 1. 3√3
      

   
   
   

   2. 3√6
      

   
   
   

   3. 6√3
      

   
   
   

   4. 5√3

      2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Tricky approach

   
   
   

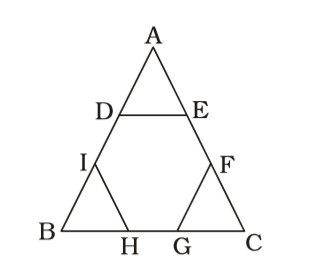
   Side of the regular hexagon =	1	× 6 = 2cm
   	3

   
   

   ∴ Area of the hexagon =	3√3	a²
   	2

   
   

   ∴ Area of the hexagon =	3√3	× 2 × 2 = 6√3 sq. cm.
   	2

   Correct Option: C

   Tricky approach

   
   
   

   Side of the regular hexagon =	1	× 6 = 2cm
   	3

   
   

   ∴ Area of the hexagon =	3√3	a²
   	2

   
   

   ∴ Area of the hexagon =	3√3	× 2 × 2 = 6√3 sq. cm.
   	2

---

---

890. The ratio of the area of a regular hexagon and an equilateral triangle having same perimeter is
     

1. 1. 2: 3
      

   
   
   

   2. 6: 1
      

   
   
   

   3. 3: 2
      

   
   
   

   4. 1: 6

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Perimeter of regular hexagon = Perimeter of equilateral triangle.
   i.e. If a side of the regular hexagon be x units, then side of triangle = 2x units.
   

   ∴ Required ratio = 6	√3	x² :	√3	(2x)²
   	4		4

   
   = 6 : 4 = 3 : 2

   Correct Option: C

   Perimeter of regular hexagon = Perimeter of equilateral triangle.
   i.e. If a side of the regular hexagon be x units, then side of triangle = 2x units.
   

   ∴ Required ratio = 6	√3	x² :	√3	(2x)²
   	4		4

   
   = 6 : 4 = 3 : 2

---