Mensuration
- ABC is a triangle with base AB. D is a point on AB such that AB = 5 and DB = 3. What is the ratio of the area of ∆ ADC to the area of ∆ ABC ?
-
View Hint View Answer Discuss in Forum
Using Rule 1,
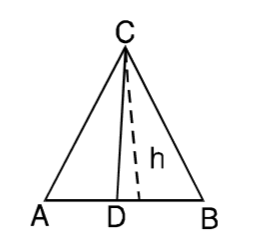
Given : AB = 5 DB = 3
∴ AD = 5 – 3 = 2
In the figure we can see that both ∆ ADC and ∆ ABC have the same height, h.Area of a triangle = 1 × base × height 2
When height is constant,
We know, Area of triangle a base,∴ Area of ∆ ADC = AD = 2 Area of ∆ ABC AB 5 Correct Option: D
Using Rule 1,

Given : AB = 5 DB = 3
∴ AD = 5 – 3 = 2
In the figure we can see that both ∆ ADC and ∆ ABC have the same height, h.Area of a triangle = 1 × base × height 2
When height is constant,
We know, Area of triangle a base,∴ Area of ∆ ADC = AD = 2 Area of ∆ ABC AB 5
- The length and breadth of a rectangular field are in the ratio 7 : 4. A path 4 m wide running all around outside has an area of 416 m² . The breadth (in m) of the field is
-
View Hint View Answer Discuss in Forum
Let length of rectangular field = 7x metre & breadth = 4x metre
Length of field with path = (7x + 8) metre
Breadth = (4x + 8) metre
∴ Area of path = (7x + 8) × (4x + 8) – 7x × 4x
= 28x² + 32x + 56x + 64 – 28x²
= 88x + 64
∴ 88x + 64 = 416
⇒ 88x = 416 – 64 = 352
⇒ x = 4
∴ Breadth of field = 16 metreliter : Using Rule 3,
Here, L = 7x, B = 4x
w = 4 m,
Area of path = 2w [L + B + 2w]
416 = 2 × 4 (7x + 4x + 2 × 4)
416 = 8 (11x + 8)
52 = 11x + 8
11x = 44 x
= 4
∴ Breadth of field = 4 × 4 = 16 mCorrect Option: D

Let length of rectangular field = 7x metre & breadth = 4x metre
Length of field with path = (7x + 8) metre
Breadth = (4x + 8) metre
∴ Area of path = (7x + 8) × (4x + 8) – 7x × 4x
= 28x² + 32x + 56x + 64 – 28x²
= 88x + 64
∴ 88x + 64 = 416
⇒ 88x = 416 – 64 = 352
⇒ x = 4
∴ Breadth of field = 16 metreliter : Using Rule 3,
Here, L = 7x, B = 4x
w = 4 m,
Area of path = 2w [L + B + 2w]
416 = 2 × 4 (7x + 4x + 2 × 4)
416 = 8 (11x + 8)
52 = 11x + 8
11x = 44 x
= 4
∴ Breadth of field = 4 × 4 = 16 m
- From a point in the interior of an equilateral triangle, the length of the perpendiculars to the three sides are 6 cm, 8 cm and 10 cm respectively. The area of the triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 6,
Let the side of the equilateral triangle ABC be x cm.
According to the question,1 × x × 6 + 1 × x × 8 + 1 × x × 10 = √3 × x² 2 2 2 4 ⇒ 3x + 4x + 5x = √3 x² 4 ⇒ √3 x = 12 4 ⇒ x = 12 × 4 = 16√3 cm √3
∴ Area of ∆ ABC⇒ √3 × (16√3)² = 192√3 cm² 4 Correct Option: C
Using Rule 1 and 6,
Let the side of the equilateral triangle ABC be x cm.
According to the question,1 × x × 6 + 1 × x × 8 + 1 × x × 10 = √3 × x² 2 2 2 4 ⇒ 3x + 4x + 5x = √3 x² 4 ⇒ √3 x = 12 4 ⇒ x = 12 × 4 = 16√3 cm √3
∴ Area of ∆ ABC⇒ √3 × (16√3)² = 192√3 cm² 4
- A lawn is in the form of a rectangle having its breadth and length in the ratio 3 : 4. The area of the lawn is 1/12 hectare. The breadth of the lawn is
-
View Hint View Answer Discuss in Forum
Using Rule 9,
= 1 hectare = 1 × 10000 sq.metre 12 12 = 25000 sq metre 3 ∴ 3x × 4x = 25000 sq metre 3 ⇒ x² = 25000 ⇒ x = 50 3 × 3 × 4 6 ⇒ Width = 3x = 3 × 50 6
= 25 metreCorrect Option: A
Using Rule 9,
= 1 hectare = 1 × 10000 sq.metre 12 12 = 25000 sq metre 3 ∴ 3x × 4x = 25000 sq metre 3 ⇒ x² = 25000 ⇒ x = 50 3 × 3 × 4 6 ⇒ Width = 3x = 3 × 50 6
= 25 metre
- In measuring the sides of a rectangle, there is an excess of 5% on one side and 2% deficit on the other. Then the error percent in the area is
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Required percentage = 
x + y + xy 
% 100 Negative sign for decrease = 
5 - 2 - 5 × 2 
% = 2.9% 100 Correct Option: C
Using Rule 10,
Required percentage = 
x + y + xy 
% 100 Negative sign for decrease = 
5 - 2 - 5 × 2 
% = 2.9% 100

