616. If the sides of an equilateral triangle be increased by 1 m its area is increased by 3 sq. metre. The length of any of its sides is
     

1. 1. 2 metre
      

   
   
   

   2. 5/2 metre
      

   
   
   

   3. 3/2 metre
      

   
   
   

   4. 3 metre

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 6,
   Side of equilateral triangle = x metre
   ∴ Difference of area = √3
   

   ⇒	√3	[(x + 1)² - x²]√3
   	4

   
   ⇒ x² +2x + 1 – x² = 4
   ⇒ 2x + 1 = 4
   ⇒ 2x = 3 ⇒ x = 3/2 metre

   Correct Option: C

   Using Rule 6,
   Side of equilateral triangle = x metre
   ∴ Difference of area = √3
   

   ⇒	√3	[(x + 1)² - x²]√3
   	4

   
   ⇒ x² +2x + 1 – x² = 4
   ⇒ 2x + 1 = 4
   ⇒ 2x = 3 ⇒ x = 3/2 metre

---

617. A straight line parallel to the base BC of the triangle ABC intersects AB and AC at the points D and E respectively. If the area of the ∆ABE be 36 sq.cm, then the area of the ∆ACD is
     

1. 1. 18 sq.cm
      

   
   
   

   2. 36 sq.cm
      

   
   
   

   3. 18 cm
      

   
   
   

   4. 36 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
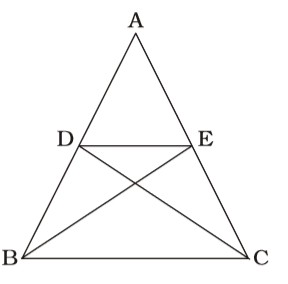
   ∆DBC and ∆EBC lie on the same base and between same parallel lines.
   ∴ ∆DBC = ∆BEC
   ⇒ ∆ABC ~ ∆DBC
   ⇒ ∆ABC ~ ∆BEC
   ⇒ ∆ADE = ∆ABE = 36 sq.cm

   Correct Option: B

   
   ∆DBC and ∆EBC lie on the same base and between same parallel lines.
   ∴ ∆DBC = ∆BEC
   ⇒ ∆ABC ~ ∆DBC
   ⇒ ∆ABC ~ ∆BEC
   ⇒ ∆ADE = ∆ABE = 36 sq.cm

---

---

618. If area of an equilateral triangle is a and height b, then value of b²/a is :
     

1. 1. 3
      

   
   
   

   2. 1/3
      

   
   
   

   3. √3
      

   
   
   

   4. 1/√3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 1,
   
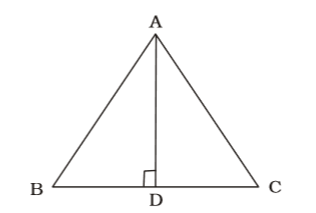
   AD = b
   Let BD = DC = x
   Each angle = 60° [∵ ∆ is equilateral]
   

   ∴ tan 60° =	AD
   	BD

   
   

   ⇒ √3 =	b	⇒ x =	b
   	x		√3

   
   

   ⇒ BC = 2x =	2b
   	√3

   
   

   ∴ Area of the triangle =	1	× BC × AD
   	2

   
   

   a =	1	×	2b	× b
   	2		√3

   
   

   ⇒	b²	= √3
   	a

   
   Let AB = BC = AC = S Area of equilateral ∆ i.e. a
   

   =	√3	S²
   	4

   
   Also AD (height)
   

   √S² -		S		²	= √S² -	S²	= √	3S²
   		2				4		4

   
   

   ⇒ b =	√3S	∴	2b²
   	2		a

   
   

   =		√3S		²
   		2
   	√3	S²
   	4

   
   

   =	3S²	×	4
   	4		√3S²

   
   

   =	3	= √3
   	√3

   Correct Option: C

   Using Rule 1,
   
   AD = b
   Let BD = DC = x
   Each angle = 60° [∵ ∆ is equilateral]
   

   ∴ tan 60° =	AD
   	BD

   
   

   ⇒ √3 =	b	⇒ x =	b
   	x		√3

   
   

   ⇒ BC = 2x =	2b
   	√3

   
   

   ∴ Area of the triangle =	1	× BC × AD
   	2

   
   

   a =	1	×	2b	× b
   	2		√3

   
   

   ⇒	b²	= √3
   	a

   
   Let AB = BC = AC = S Area of equilateral ∆ i.e. a
   

   =	√3	S²
   	4

   
   Also AD (height)
   

   √S² -		S		²	= √S² -	S²	= √	3S²
   		2				4		4

   
   

   ⇒ b =	√3S	∴	2b²
   	2		a

   
   

   =		√3S		²
   		2
   	√3	S²
   	4

   
   

   =	3S²	×	4
   	4		√3S²

   
   

   =	3	= √3
   	√3

---

619. ABC is an isosceles right angled triangle with ∠B = 90°. On the sides AC and AB, two equilateral triangles ACD and ABE have been constructed. The ratio of area of ∆ABE and ∆ACD is

1. 1. 1 : 3
      

   
   
   

   2. 2 : 3
      

   
   
   

   3. 1 : 2
      

   
   
   

   4. 1 : √2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Using Rule 6,
   
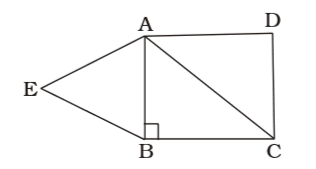
   AB = x units
   BC = x units
   AC = 2 x units [Using Pythagorus]
   

   ∴	∆ABE
   	∆ACD

   
   

   =	√3	x²
   	4
   	√3	(√3x)²
   	4

   
   

   =	1	= 1 : 2
   	2

   Correct Option: C

   Using Rule 6,
   
   AB = x units
   BC = x units
   AC = 2 x units [Using Pythagorus]
   

   ∴	∆ABE
   	∆ACD

   
   

   =	√3	x²
   	4
   	√3	(√3x)²
   	4

   
   

   =	1	= 1 : 2
   	2

---

---

620. Two triangles ABC and DEF are similar to each other in which AB = 10 cm, DE = 8 cm. Then the ratio of the area of triangles ABC and DEF is
     

1. 1. 4 : 5
      

   
   
   

   2. 25 : 16
      

   
   
   

   3. 64 : 125
      

   
   
   

   4. 4 : 7

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∆ABC	=	AB²	=	100	=	25
   ∆DEF		DE²		64		16

   
   = 25 : 16
   [∵ ∆ABC ~ ∆DEF]

   Correct Option: B

   ∆ABC	=	AB²	=	100	=	25
   ∆DEF		DE²		64		16

   
   = 25 : 16
   [∵ ∆ABC ~ ∆DEF]

---