-
If area of an equilateral triangle is a and height b, then value of b²/a is :
-
- 3
- 1/3
- √3
- 1/√3
- 3
Correct Option: C
Using Rule 1,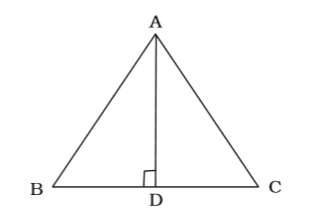
AD = b
Let BD = DC = x
Each angle = 60° [∵ ∆ is equilateral]
| ∴ tan 60° = | |
| BD |
| ⇒ √3 = | ⇒ x = | ||
| x | √3 |
| ⇒ BC = 2x = | |
| √3 |
| ∴ Area of the triangle = | × BC × AD | |
| 2 |
| a = | × | × b | ||
| 2 | √3 |
| ⇒ | = √3 | |
| a |
Let AB = BC = AC = S Area of equilateral ∆ i.e. a
| = | S² | |
| 4 |
Also AD (height)
| √S² - |  |  | ² | = √S² - | = √ | |||
| 2 | 4 | 4 |
| ⇒ b = | ∴ | ||
| 2 | a |
| = |  |  | ² | |
| 2 | ||||
| S² | ||||
| 4 | ||||
| = | × | ||
| 4 | √3S² |
| = | = √3 | |
| √3 |

