Mensuration
- If the height of a cylinder is 4 times its circumference, the volume of the cylinder in terms of its circumference c, is
-
View Hint View Answer Discuss in Forum
If the radius of base of cylinder be r units, then,
Height = 4 × 2πr = 8πr units
∴ 2πr = c∴ r = c and h = 4c 2π
∴ Volume of cylinder = πr²h= πc² × 4c 4π² = c³ cubic units π Correct Option: C
If the radius of base of cylinder be r units, then,
Height = 4 × 2πr = 8πr units
∴ 2πr = c∴ r = c and h = 4c 2π
∴ Volume of cylinder = πr²h= πc² × 4c 4π² = c³ cubic units π
- Base of a right pyramid is a square whose area is 324 sq metre. If the volume of the pyramid is 1296 cu.metre, then the area (in sq. metre) of the slant surface is
-
View Hint View Answer Discuss in Forum
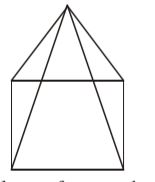
= 1 × area of base × height 3 ⇒ 1296 = 1 × 324 × h 3 ⇒ h = 1296 × 3 12 metre 324
∴ Side of square base = √324 = 18 metre∴ Slant height = √12² + >
18 
² 2
= √12² + 9² = √144 + 81
= √225 = 15 metre∴ Area of the lateral surfaces = 1 × perimeter of base × slant height 2 = 1 × 4 × 18 × 15 2
= 540 sq.metre.Correct Option: B

= 1 × area of base × height 3 ⇒ 1296 = 1 × 324 × h 3 ⇒ h = 1296 × 3 12 metre 324
∴ Side of square base = √324 = 18 metre∴ Slant height = √12² + >
18 
² 2
= √12² + 9² = √144 + 81
= √225 = 15 metre∴ Area of the lateral surfaces = 1 × perimeter of base × slant height 2 = 1 × 4 × 18 × 15 2
= 540 sq.metre.
- If the surface areas of two spheres are in the ratio 9 : 16, the ratio of their volumes is
-
View Hint View Answer Discuss in Forum
Radii of spheres = r1 and r2 units According to the question
4πr1² = 9 4πr2² 16 ⇒ r1² = 9 r2² 16 ⇒ r1² = √ 9 = 3 r2² 16 4 ∴ Ratio of their volumes = 4 πr1³ 3 4 πr2³ 3 = 
r1 
³ = 
3 
³ = 27 r2 4 64 Correct Option: B
Radii of spheres = r1 and r2 units According to the question
4πr1² = 9 4πr2² 16 ⇒ r1² = 9 r2² 16 ⇒ r1² = √ 9 = 3 r2² 16 4 ∴ Ratio of their volumes = 4 πr1³ 3 4 πr2³ 3 = 
r1 
³ = 
3 
³ = 27 r2 4 64
- The volume of a right circular cone is equal to the volume of a right circular cylinder. The height and the radius of the cylinder are 9 cm and 20 cm respectively. If the height of the cone is 108 cm, then its radius, (in cm) is
-
View Hint View Answer Discuss in Forum
Volume of cylinder = πr²h
= (π × 20 × 20 × 9)cu.cm.
= 3600 π cu.cm.
∴ Volume of cone = 3600π cu.cm.⇒ 1 πR²H = 3600π 3 ⇒ 1 × R² × 108 = 3600 3 ⇒ R² = 3600 × 3 = 100 108
→ R = √100 = 10 cm.Correct Option: D
Volume of cylinder = πr²h
= (π × 20 × 20 × 9)cu.cm.
= 3600 π cu.cm.
∴ Volume of cone = 3600π cu.cm.⇒ 1 πR²H = 3600π 3 ⇒ 1 × R² × 108 = 3600 3 ⇒ R² = 3600 × 3 = 100 108
→ R = √100 = 10 cm.
- A right circular cone and a right circular cylinder have the same base and their heights are in the ratio 2 : 3. The ratio of their volumes will be
-
View Hint View Answer Discuss in Forum
Radius of the base of the cylinder = radius of the base of cone
= x unitsVolume of cone Volume of cylinder = 1 πr³H 3 πr³h = 1 . H = 1 × 2 = 2 : 9 3 h 3 3 Correct Option: D
Radius of the base of the cylinder = radius of the base of cone
= x unitsVolume of cone Volume of cylinder = 1 πr³H 3 πr³h = 1 . H = 1 × 2 = 2 : 9 3 h 3 3

