Mensuration
- The diameter of the front wheel of an engine is 2x cm and that of rear wheel is 2y cm. To cover the same distance, find the number of times the rear wheel will revolve when the front wheel revolves ‘n’ times.
-
View Hint View Answer Discuss in Forum
Number of revolutions of rear wheel
= m (let)
Distance covered by front wheel in 1 revolution
= π × diameter
= 2πx cm.
Distance covered by rear wheel in 1 revolution = 2πy cm
∴ 2πx × n = 2πy × m⇒ m = nx y Correct Option: C
Number of revolutions of rear wheel
= m (let)
Distance covered by front wheel in 1 revolution
= π × diameter
= 2πx cm.
Distance covered by rear wheel in 1 revolution = 2πy cm
∴ 2πx × n = 2πy × m⇒ m = nx y
- A right pyramid stands on a square base of diagonal 10√2 cm. If the height of the pyramid is 12 cm, the area (in cm²) of its slant surface is
-
View Hint View Answer Discuss in Forum
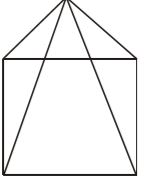
Side of square base = 1 × 10√2 = 10 cm. √2
Slant height = √5² + 12² = 13 cm∴ Area of the lateral surface = 1 × perimeter of base × slant height 2 = 1 × 40 × 13 = 260 sq.cm. 2 Correct Option: D

Side of square base = 1 × 10√2 = 10 cm. √2
Slant height = √5² + 12² = 13 cm∴ Area of the lateral surface = 1 × perimeter of base × slant height 2 = 1 × 40 × 13 = 260 sq.cm. 2
- If the altitude of a right prism is 10 cm and its base is an equilateral triangle of side 12 cm, then its total surface area (in cm²) is
-
View Hint View Answer Discuss in Forum
Total surface area = Perimeter of base × height + 2 × area of base
= 36 × 10 + 2 × √3 × 12 × 12 4
= 360 + 72√3
= 72 ( 5 + √3) sq. cmCorrect Option: D
Total surface area = Perimeter of base × height + 2 × area of base
= 36 × 10 + 2 × √3 × 12 × 12 4
= 360 + 72√3
= 72 ( 5 + √3) sq. cm
- In ∆ABC, D, E and F are the mid-points of sides BC, CA and AB respectively. What is the area of quadrilateral BDEF ?
-
View Hint View Answer Discuss in Forum
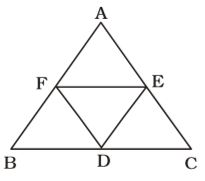
D, E are the mid-points on BC and AC respectively.
∴ DE || BA Þ DE || BF
Similarly, FE || BD
∴ BDEF is a parallelogram.
Similarly, DCEF and AFDE are parallelograms.
∴ ∆BDF = ∆DEF
∆DCE = ∆DEF
and ∆AFE = ∆DEF
∴ ∆BDF = ∆DCE = ∆AFE = DDEF⇒ ∆DEF = 1 ∆ABC 4
∴ Quadrilateral BDEF = 2 × DDEF
⇒ Quadrilateral BDEF= 2 × 1 ∆ABC 4 = 1 ∆ABC 2 Correct Option: B

D, E are the mid-points on BC and AC respectively.
∴ DE || BA Þ DE || BF
Similarly, FE || BD
∴ BDEF is a parallelogram.
Similarly, DCEF and AFDE are parallelograms.
∴ ∆BDF = ∆DEF
∆DCE = ∆DEF
and ∆AFE = ∆DEF
∴ ∆BDF = ∆DCE = ∆AFE = DDEF⇒ ∆DEF = 1 ∆ABC 4
∴ Quadrilateral BDEF = 2 × DDEF
⇒ Quadrilateral BDEF= 2 × 1 ∆ABC 4 = 1 ∆ABC 2
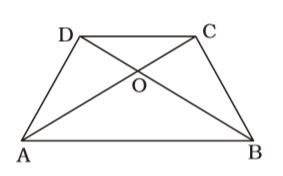
- ABCD is a trapezium in which AB||DC and AB = 2DC. Then what is the ratio between the areas of ∆AOB and ∆COD respectively ?
-
View Hint View Answer Discuss in Forum
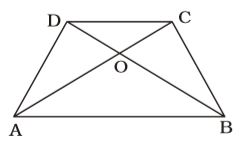
In ∆AOB and ∆COD,
∠AOB = ∠COD and ∠OAB = ∠OCD
By AA-similarly theorem, ∆AOB ~ ∆COD∴ ∆AOB = AB² ∆COD CD² = (2DC)² = 4 CD² 1 Correct Option: A

In ∆AOB and ∆COD,
∠AOB = ∠COD and ∠OAB = ∠OCD
By AA-similarly theorem, ∆AOB ~ ∆COD∴ ∆AOB = AB² ∆COD CD² = (2DC)² = 4 CD² 1

