Mensuration
- Two isosceles triangles have equal vertical angles and their areas are in the ratio 9:16. Then the ratio of their corresponding heights is
-
View Hint View Answer Discuss in Forum

∠A = ∠D
∴ ∠B = ∠E; ∠C = ∠F
∴ Ratio of altitudes =∴ Ratio of altitudes = √ 9 = 3 : 4 16 Correct Option: D

∠A = ∠D
∴ ∠B = ∠E; ∠C = ∠F
∴ Ratio of altitudes =∴ Ratio of altitudes = √ 9 = 3 : 4 16
- The amount of rice produced in a square field of side 50 m is 750 kg. The amount of rice produced in a similar square field of side 100 m will be
-
View Hint View Answer Discuss in Forum
Area of the field with side 50 m = 50 × 50 = 2500 sq.
metre Area of the field of side 100 m
= 100 × 100
= 10000 sq. metre
∵ 2500 sq. metre ≡ 750 kg.
∴ 10000 sq. metre≡ 750 × 10000 kg. 2500
= 3000 kg.Correct Option: B
Area of the field with side 50 m = 50 × 50 = 2500 sq.
metre Area of the field of side 100 m
= 100 × 100
= 10000 sq. metre
∵ 2500 sq. metre ≡ 750 kg.
∴ 10000 sq. metre≡ 750 × 10000 kg. 2500
= 3000 kg.
- The time required for a boy to travel along the external and internal boundaries of a circular path are in the ratio 20 : 19. If the width of the path be 5 metres, the internal diameter is :
-
View Hint View Answer Discuss in Forum
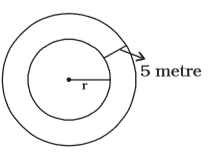
More distance, more time (speed is constant)∴ 2π (r + 5) = 20 2πr 19 ⇒ (r + 5) = 20 r 19
⇒ 20r = 19r + 95
⇒ 20r – 19r = 95
⇒ r = 95 metre
∴ Internal diameter = (2 × 95) metre = 190 metreCorrect Option: D

More distance, more time (speed is constant)∴ 2π (r + 5) = 20 2πr 19 ⇒ (r + 5) = 20 r 19
⇒ 20r = 19r + 95
⇒ 20r – 19r = 95
⇒ r = 95 metre
∴ Internal diameter = (2 × 95) metre = 190 metre
- In triangle ABC, DE || BC where D is a point on AB and E is a point on AC. DE divides the area of ∆ABC into two equal parts. Then DB : AB is equal to
-
View Hint View Answer Discuss in Forum
DE || BC Area of ∆ADE = Area of quadrilateral BDEC
⇒ Area of ∆ABC = 2 × Area of ∆ADE
In ∆ADE and ∆ABC,
∠D = ∠B ; ∠E = ∠C
∴ ∆ADE ~ ∆ABC∴ Area of ∆ABC = AB² Area of ∆ADE AD² ⇒ AB² = 2 ⇒ AB = √2AD AD²
⇒ AB = √2(AB – DB)
⇒ √2AB – AB = √2 DB
⇒ AB (√2 – 1) = √2DB⇒ DB = √2 - 1 AB √2 Correct Option: C
DE || BC Area of ∆ADE = Area of quadrilateral BDEC
⇒ Area of ∆ABC = 2 × Area of ∆ADE
In ∆ADE and ∆ABC,
∠D = ∠B ; ∠E = ∠C
∴ ∆ADE ~ ∆ABC∴ Area of ∆ABC = AB² Area of ∆ADE AD² ⇒ AB² = 2 ⇒ AB = √2AD AD²
⇒ AB = √2(AB – DB)
⇒ √2AB – AB = √2 DB
⇒ AB (√2 – 1) = √2DB⇒ DB = √2 - 1 AB √2
- The centroid of a ∆ABC is G. The area of ∆ABC is 60 cm². The area of ∆GBC is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
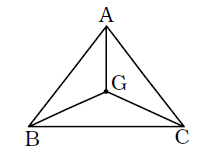
∆GBC = ∆ACG = ∆AGB∴ Area of ∆GBC = 1 × Area of ∆ABC 3 ∴ Area of ∆GBC = 1 × 60 = 20 sq. cm. 3 Correct Option: D
Using Rule 1,

∆GBC = ∆ACG = ∆AGB∴ Area of ∆GBC = 1 × Area of ∆ABC 3 ∴ Area of ∆GBC = 1 × 60 = 20 sq. cm. 3
-