Mensuration
- If the perimeter of an equilateral triangle be 18 cm, then the length of each median is
-
View Hint View Answer Discuss in Forum
Perimeter of equilateral triangle = 3 × side
∴ 3 × side = 18⇒ Side = 18 = 6 cm. 3 ∴ Length of median = √3 × side 2 = √3 × 6 = 3√3 cm 2 Correct Option: C
Perimeter of equilateral triangle = 3 × side
∴ 3 × side = 18⇒ Side = 18 = 6 cm. 3 ∴ Length of median = √3 × side 2 = √3 × 6 = 3√3 cm 2
- Two equal maximum sized circular plates are cut off from a circular paper sheet of circumference 352 cm. Then the circumference of each circular plate is
-
View Hint View Answer Discuss in Forum
Using Rule 14,
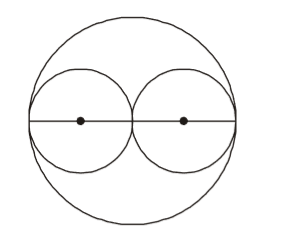
Radius of circular paper sheet Circumference = 352 2π 2π = 352 2 × 22 7 = 352 × 7 = 56 cm 2 × 22 ∴ Radius of each plate = 56 = 28 cm 2
∴ Circumference of each circular plate = 2πr= 2 × 22 × 28 = 176 cm 7 Correct Option: A
Using Rule 14,

Radius of circular paper sheet Circumference = 352 2π 2π = 352 2 × 22 7 = 352 × 7 = 56 cm 2 × 22 ∴ Radius of each plate = 56 = 28 cm 2
∴ Circumference of each circular plate = 2πr= 2 × 22 × 28 = 176 cm 7
- If diagonals of a rhombus are 24 cm and 32 cm, then perimeter of that rhombus is
-
View Hint View Answer Discuss in Forum
Using Rule 12,

AC = 24 cm = d2
BD = 32 cm = d1
∴ OD = 16 cm
OC = 12 cm
∠ COD = 90°
∴ CD = √OC² + OD²
= √12² + 16²
= √144 + 256
= √400 = 20 cm
∴ Perimeter of rhombus = 4 × CD = 4 × 20 = 80 cmCorrect Option: A
Using Rule 12,

AC = 24 cm = d2
BD = 32 cm = d1
∴ OD = 16 cm
OC = 12 cm
∠ COD = 90°
∴ CD = √OC² + OD²
= √12² + 16²
= √144 + 256
= √400 = 20 cm
∴ Perimeter of rhombus = 4 × CD = 4 × 20 = 80 cm
- The inradius of an equilateral triangle is √3 cm, then the perimeter of that triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 18,
In-radius = Side 2√3 ∴ √3 = Side 2√3
⇒ Side = 2√3 × √3 = 6 cm
∴ Perimeter of equilateral = 3 × 6 = 18 cmCorrect Option: A
Using Rule 18,
In-radius = Side 2√3 ∴ √3 = Side 2√3
⇒ Side = 2√3 × √3 = 6 cm
∴ Perimeter of equilateral = 3 × 6 = 18 cm
- Length of a side of a square inscribed in a circle is a√2 units. The circumference of the circle is
-
View Hint View Answer Discuss in Forum
Using Rule 10 and 14,

Side of a square = AB = √2 a units
∴ AC = Diagonal = √2 × √2 a
= 2 a units
= Diameter (d) of circle
∴ Circumference of circle = π × d = π × 2 a = 2π a unitsCorrect Option: A
Using Rule 10 and 14,

Side of a square = AB = √2 a units
∴ AC = Diagonal = √2 × √2 a
= 2 a units
= Diameter (d) of circle
∴ Circumference of circle = π × d = π × 2 a = 2π a units

