Mensuration
- ABCD is a parallelogram. P and Q are the mid-points of BC and CD respectively. What is the ratio between the area of ∆APQ to that of the parallelogram ABCD?
-
View Hint View Answer Discuss in Forum

In ∆BCD,
PQ || BD and PQ = 1/2 BD⇒ ar (∆CPQ) = 1 ar (BDC) 4
⇒ ar (∆CPQ)= 1 (||gmABCD) 8 
∵ 1 ar (||gmABCD) = ar (∆BCD) 
2 BP = 1 BC 2 ∴ ar (∆ ABP) = 1 ar (||gmABCD) 4
Similarly, ar (∆AQD)= 1 ar (||gmABCD) 4
∴ ar (∆APQ) = ar (gm ABCD )– [ar ∆ABP + ar (∆AQD) + ar (∆CPQ)]= ar (||gmABCD) – 
1 + 1 + 1 
ar (||gmABCD) 4 4 8 = 
1 - 5 
ar (||gmABCD) 8 = 3 ar (||gmABCD) 8 Correct Option: B

In ∆BCD,
PQ || BD and PQ = 1/2 BD⇒ ar (∆CPQ) = 1 ar (BDC) 4
⇒ ar (∆CPQ)= 1 (||gmABCD) 8 
∵ 1 ar (||gmABCD) = ar (∆BCD) 
2 BP = 1 BC 2 ∴ ar (∆ ABP) = 1 ar (||gmABCD) 4
Similarly, ar (∆AQD)= 1 ar (||gmABCD) 4
∴ ar (∆APQ) = ar (gm ABCD )– [ar ∆ABP + ar (∆AQD) + ar (∆CPQ)]= ar (||gmABCD) – 
1 + 1 + 1 
ar (||gmABCD) 4 4 8 = 
1 - 5 
ar (||gmABCD) 8 = 3 ar (||gmABCD) 8
- A solid sphere of diameter 6 cms is melted and shaped as a hollow cylinder of outer radius 5 cms and height 4 cms. What is the thickness of the cylinder ?
-
View Hint View Answer Discuss in Forum
Volume of sphere = 4 πr³ = 4 π × (3)³ cu.cm. 3 3
Let the thickness of cylinder be x cm.
∴ Its internal radius = (5 – x) cm
Now,volume of cylinder = 4 π × 27 3
⇒ π{(5)² – (5 – x)²} × 4= 4 π × 27 3
⇒ 25 – (25 + x² – 10x) = 9
⇒ x² – 10x + 9 = 0
⇒ x² – 9x – x + 9 = 0
⇒ x (x – 9) – 1 (x – 9) = 0
⇒ (x – 1) (x – 9) = 0
⇒ x = 1 because x ≠ 9Correct Option: D
Volume of sphere = 4 πr³ = 4 π × (3)³ cu.cm. 3 3
Let the thickness of cylinder be x cm.
∴ Its internal radius = (5 – x) cm
Now,volume of cylinder = 4 π × 27 3
⇒ π{(5)² – (5 – x)²} × 4= 4 π × 27 3
⇒ 25 – (25 + x² – 10x) = 9
⇒ x² – 10x + 9 = 0
⇒ x² – 9x – x + 9 = 0
⇒ x (x – 9) – 1 (x – 9) = 0
⇒ (x – 1) (x – 9) = 0
⇒ x = 1 because x ≠ 9
- The sum of length, breadth and height of a rectangular parallelopiped is 20 cm. and its whole surface area is 264 sq. cm. Find the area of the square whose side is equal to the length of the diagonal of the parallelopiped.
-
View Hint View Answer Discuss in Forum
Let the length, breadth and height of the parallelopiped bea, b and c cm respectively.
∴ a + b + c = 20
2 (ab + bc + ca) = 264
∴ (a + b + c)² = a² + b² + c² + 2 (ab + bc + ca)
⇒ 400 = a² + b² + c² + 264
⇒ a² + b² + c² = 400 – 264 = 136 sq. cm.
Area of square = (√a² + b² + c²)² = 136 sq. cm.Correct Option: A
Let the length, breadth and height of the parallelopiped bea, b and c cm respectively.
∴ a + b + c = 20
2 (ab + bc + ca) = 264
∴ (a + b + c)² = a² + b² + c² + 2 (ab + bc + ca)
⇒ 400 = a² + b² + c² + 264
⇒ a² + b² + c² = 400 – 264 = 136 sq. cm.
Area of square = (√a² + b² + c²)² = 136 sq. cm.
- Find the ratio of the areas of squares circumscribed about and inscribed in the same circle.
-
View Hint View Answer Discuss in Forum
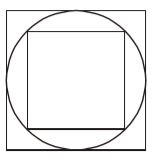
Let the diameter of circle be d units.
∴ Diagonal of the inscribed square = dIts area = 1 d² sq. units. 2
Side of the circumscribed square = d units
∴ Its area = d² sq. unitsRequired ratio = d² : 1 d² = 2 : 1 2 Correct Option: B

Let the diameter of circle be d units.
∴ Diagonal of the inscribed square = dIts area = 1 d² sq. units. 2
Side of the circumscribed square = d units
∴ Its area = d² sq. unitsRequired ratio = d² : 1 d² = 2 : 1 2
- A cube and a sphere have equal surface areas. Find the ratio of their volumes.
-
View Hint View Answer Discuss in Forum
Let the edge of cube be x units and radius of sphere be y units.
∴ Surface area of cube = surface area of sphere
⇒ 6x² = 4πy²⇒ x² = 4π = 2π y² 6 3 ⇒ x = √ 2π ⇒ x : y = √2π : √3 y 3
2⇒ Volume of cube : Volume of sphere= x³ : 4 πy³ = 3x³ : 4πy³ 3
= 3 × 2π√2π : 4π × 3 × √3
= π√2π : 2√3
= √π : √6Correct Option: B
Let the edge of cube be x units and radius of sphere be y units.
∴ Surface area of cube = surface area of sphere
⇒ 6x² = 4πy²⇒ x² = 4π = 2π y² 6 3 ⇒ x = √ 2π ⇒ x : y = √2π : √3 y 3
2⇒ Volume of cube : Volume of sphere= x³ : 4 πy³ = 3x³ : 4πy³ 3
= 3 × 2π√2π : 4π × 3 × √3
= π√2π : 2√3
= √π : √6

