-
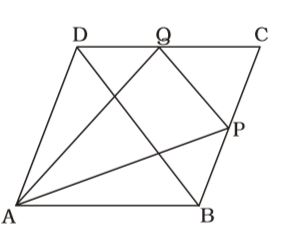
ABCD is a parallelogram. P and Q are the mid-points of BC and CD respectively. What is the ratio between the area of ∆APQ to that of the parallelogram ABCD?
-
- 3 : 7
- 3 : 8
- 3 : 5
- 4 : 9
- 3 : 7
Correct Option: B
In ∆BCD,
PQ || BD and PQ = 1/2 BD
| ⇒ ar (∆CPQ) = | ar (BDC) | |
| 4 |
⇒ ar (∆CPQ)
| = | (||gmABCD) | |
| 8 |
 | ∵ | ar (||gmABCD) = ar (∆BCD) |  | |
| 2 |
| BP = | BC | |
| 2 |
| ∴ ar (∆ ABP) = | ar (||gmABCD) | |
| 4 |
Similarly, ar (∆AQD)
| = | ar (||gmABCD) | |
| 4 |
∴ ar (∆APQ) = ar (gm ABCD )– [ar ∆ABP + ar (∆AQD) + ar (∆CPQ)]
| = ar (||gmABCD) – |  | + | + |  | ar (||gmABCD) | |||
| 4 | 4 | 8 |
| = |  | 1 - |  | ar (||gmABCD) | |
| 8 |
| = | ar (||gmABCD) | |
| 8 |

