Mensuration
- Let C1 and C2 be the inscribed and circumscribed circles of a triangle with sides 3cm, 4cm and 5cm then
area of C1 is area of C2
-
View Hint View Answer Discuss in Forum
Using Rule 1 and 14,
It is a right angled triangle.
Radius of circum circle C2
= 5/2 cm. because
AC = Diameter of circleSemi-perimeter of ∆ABC(s) = 3 + 4 + 5 = 6cm. 2 Area of ∆ABC = 1 × 3 × 4 = 6 sq.cm. 2 ∴ In-radius = ∆ = 6 = 1 cm. s 6 ∴ Area of C1 = π × 1² Area of C2 π × 
5 
² 2 = 1 25 4 = 4 25 Correct Option: B
Using Rule 1 and 14,
It is a right angled triangle.
Radius of circum circle C2
= 5/2 cm. because
AC = Diameter of circleSemi-perimeter of ∆ABC(s) = 3 + 4 + 5 = 6cm. 2 Area of ∆ABC = 1 × 3 × 4 = 6 sq.cm. 2 ∴ In-radius = ∆ = 6 = 1 cm. s 6 ∴ Area of C1 = π × 1² Area of C2 π × 
5 
² 2 = 1 25 4 = 4 25
- If the altitude of an equilateral triangle is 12√3 cm, then its area would be :
-
View Hint View Answer Discuss in Forum
Using Rule 6, A
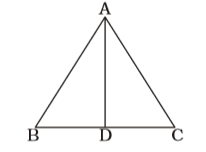
AD = 12√3 cm.
AB = 2x cm. (let)
BD = x cm.
From ∆ABD,
AD = √AB² - BD²
= √(2x)² - x²
= √4x² - x²
= √3x²
= √3x
∴ √3x = 12√3
⇒ x = 12 cm.
∴ AB = 2x = 2 × 12 = 24 cm.∴ Area of ∆ABC = √3 × side² 4 = √3 × 24 × 24 4
= 144√3 sq. cm.Correct Option: B
Using Rule 6, A

AD = 12√3 cm.
AB = 2x cm. (let)
BD = x cm.
From ∆ABD,
AD = √AB² - BD²
= √(2x)² - x²
= √4x² - x²
= √3x²
= √3x
∴ √3x = 12√3
⇒ x = 12 cm.
∴ AB = 2x = 2 × 12 = 24 cm.∴ Area of ∆ABC = √3 × side² 4 = √3 × 24 × 24 4
= 144√3 sq. cm.
- Given that : ∆ABC ~ ∆PQR, If
area (∆ PQR) = 256 area (∆ ABC) 441
and PR = 12 cm, then AC is equal to
-
View Hint View Answer Discuss in Forum
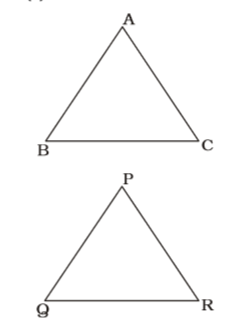
The ratio of the areas of two similar triangles is equal to the ratio of squares of any two corresponding sides.∴ Area of ∆PQR = PR² Area of ∆ABC AC² ⇒ PR² = 256 AC² 441 ⇒ 12² = 256 AC² 441
Taking square roots of both sides,12 = 16 AC 21
⇒ 16 × AC = 12 × 21⇒ AC = 12 × 21 = 63 16 4
= 15.75 cm.Correct Option: A

The ratio of the areas of two similar triangles is equal to the ratio of squares of any two corresponding sides.∴ Area of ∆PQR = PR² Area of ∆ABC AC² ⇒ PR² = 256 AC² 441 ⇒ 12² = 256 AC² 441
Taking square roots of both sides,12 = 16 AC 21
⇒ 16 × AC = 12 × 21⇒ AC = 12 × 21 = 63 16 4
= 15.75 cm.
- ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB = 110° and ∠CBD = 30°, then ∠ADB measures
-
View Hint View Answer Discuss in Forum
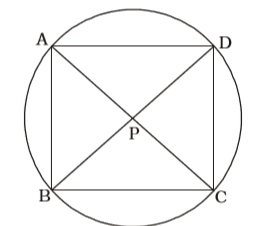
∠APB = 110° = ∠CPD
∴ ∠APD = 180° – 110° = 70° = ∠BPC
∴ ∠PCB = 180° – 70° – 30° = 80°
Angles subtended by same arcs at the circumference are equal.
∴ ∠ACB or ∠PCB = ∠ADB = 80°Correct Option: D

∠APB = 110° = ∠CPD
∴ ∠APD = 180° – 110° = 70° = ∠BPC
∴ ∠PCB = 180° – 70° – 30° = 80°
Angles subtended by same arcs at the circumference are equal.
∴ ∠ACB or ∠PCB = ∠ADB = 80°
- A circular swimming pool is surrounded by a concrete wall 4m wide. If the area of the concrete wall surrounding the pool is 11/25 that of the pool, then the radius (in m) of the pool is :
-
View Hint View Answer Discuss in Forum
Let the radius of swimming pool be r metre.
Breadth of shaded part = 4 metre
∴ OB = (r + 4) metre According to the question,
π × OB² – π × OA²= 11 π × OA² 25 ⇒ (r + 4)² – r² = 11 r² 25 ⇒ r² + 8r + 16 - r² = 11 r² 25 ⇒ 8r + 16 = 11 r² 25
⇒ 200r + 400 = 11r²
⇒ 11r² – 200r – 400 = 0
⇒ 11r² – 220r + 20r – 400 = 0
⇒ 11r (r – 20) + 20 (r – 20) = 0
⇒ (r – 20) (11r + 20) = 0
⇒ r = 20 metre becauser ≠ - 20 metre 11 Correct Option: D
Let the radius of swimming pool be r metre.
Breadth of shaded part = 4 metre
∴ OB = (r + 4) metre According to the question,
π × OB² – π × OA²= 11 π × OA² 25 ⇒ (r + 4)² – r² = 11 r² 25 ⇒ r² + 8r + 16 - r² = 11 r² 25 ⇒ 8r + 16 = 11 r² 25
⇒ 200r + 400 = 11r²
⇒ 11r² – 200r – 400 = 0
⇒ 11r² – 220r + 20r – 400 = 0
⇒ 11r (r – 20) + 20 (r – 20) = 0
⇒ (r – 20) (11r + 20) = 0
⇒ r = 20 metre becauser ≠ - 20 metre 11

